
����Ŀ�����κ���y=![]() ��ͼ����x�ύ�ڵ�A�͵�B����ABΪ����x���·���������ABCD����P��x����һ���㣬����DP������P��DP�Ĵ�����y�ύ�ڵ�E��
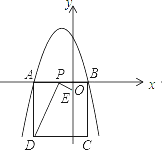
��ͼ����x�ύ�ڵ�A�͵�B����ABΪ����x���·���������ABCD����P��x����һ���㣬����DP������P��DP�Ĵ�����y�ύ�ڵ�E��
��1�����m��ֵ�������A����B�����꣮
��2������P���߶�AO����P����A��O�غϣ����˶����δ�ʱ���߶�OE�ij������ֵ�����������ֵ��
��3���Ƿ���������ĵ�P��ʹ��PED�ǵ��������Σ������ڣ��������P�����꼰��ʱ��PED��������ABCD�ص����ֵ�������������ڣ���˵�����ɣ�
���𰸡���1��m=��2��A����3��0����B��1��0������2��PΪAO�е�ʱ��OE�����ֵΪ![]() ����3�����ڣ�������.
����3�����ڣ�������.
��������
��1�����ö��κ����Ķ������m��֪������y=0���ɵó���A��B���ꣻ
��2����PA=t��-3��t��0������OP=3-t����ͼ1��֤����DAP�ס�POE���������Ʊȵõ�OE=-![]() ��Ȼ�����ö��κ��������ʽ�����⣻
��Ȼ�����ö��κ��������ʽ�����⣻
��3�����ۣ�����P��y�����ʱ����ͼ2��DE��AB��G�㣬֤����DAP�ա�POE�õ�PO=AD=4����PA=1��OE=1��������ƽ���߷��߶γɱ������������AG=![]() �������S��DAG���ɵõ���ʱ��PED��������ABCD�ص����ֵ��������P����y���Ҳ�ʱ����ͼ3��DE��AB��G�㣬DP��BC�ཻ��Q��ͬ���ɵ���DAP�ա�POE����PO=AD=4��PA=7��OE=7��������ƽ���߷��߶γɱ������������OG��BQ��Ȼ�����S�ı���DGBQ�õ���ʱ��PED��������ABCD�ص����ֵ����������P�͵�A�غ�ʱ����E�ͺ͵�O�غϣ���ʱ����PED���ǵ��������Σ�
�������S��DAG���ɵõ���ʱ��PED��������ABCD�ص����ֵ��������P����y���Ҳ�ʱ����ͼ3��DE��AB��G�㣬DP��BC�ཻ��Q��ͬ���ɵ���DAP�ա�POE����PO=AD=4��PA=7��OE=7��������ƽ���߷��߶γɱ������������OG��BQ��Ȼ�����S�ı���DGBQ�õ���ʱ��PED��������ABCD�ص����ֵ����������P�͵�A�غ�ʱ����E�ͺ͵�O�غϣ���ʱ����PED���ǵ��������Σ�
��1���߶��κ���y=��m��1��![]() ��6x+9��
��6x+9��
��m2+m=2��m��1��0��
��m=��2��
����κ�������ʽΪy=��3x2��6x+9��
��y=0��
��0=��3x2��6x+9��
��x=1��x=��3��
��A����3��0����B��1��0����
��2����PA=t����3��t��0������OP=3��t��
��DP��PE��
���DPA=��PEO��
���DAP�ס�POE��
��![]() ����
����![]() ��
��
��OE=��![]() t2+
t2+![]() t=��
t=��![]() ��t��
��t��![]() ��2+
��2+![]() ��
��
�൱t=![]() ʱ��OE�����ֵ��
ʱ��OE�����ֵ��
��PΪAO�е�ʱ��OE�����ֵΪ![]() ��
��
��3�����ڣ�
����P��y�����ʱ����ͼ1��DE��AB��G�㣬
��PD=PE����DPE=90����
���DAP�ա�POE��
��PO=AD=4��
��PA=1��OE=1��
��AD��OE��
��![]() =4��
=4��
��AG=![]() ��
��
��S��DAG=![]() ��
��![]() ��4=
��4=![]() ��
��
��P������Ϊ����4��0������ʱ��PED��������ABCD�ص����ֵ����Ϊ��![]() ��P����y���Ҳ�ʱ����ͼ2��DE��AB��G�㣬DP��BC�ཻ��Q��ͬ���ɵ���DAP�ա�POE��
��P����y���Ҳ�ʱ����ͼ2��DE��AB��G�㣬DP��BC�ཻ��Q��ͬ���ɵ���DAP�ա�POE��
��PO=AD=4��
��PA=7��OE=7��
��AD��OE��
��![]() ��
��
��OG=![]() ��
��
ͬ���ɵ�BQ=![]() ��
��
��S�ı���DGBQ=![]() ����
����![]() +1����4+
+1����4+![]() ��4��
��4��![]() =
=![]()
�൱��P������Ϊ��4��0��ʱ����ʱ��PED��������ABCD�ص����ֵ����Ϊ![]() ��
��
����P�͵�A�غϣ���ʱ����E�͵�O�غϣ���DP��OP����ʱ����PDE���ǵ��������Σ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���![]() ��ͼ����ͼ��ʾ�����н��ۣ�
��ͼ����ͼ��ʾ�����н��ۣ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��������ȷ���۵���
��������ȷ���۵���![]() ����
����![]()
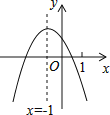
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����ϣ�������⣮
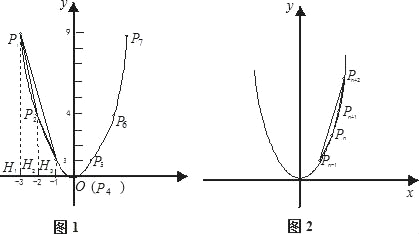
���ϣ���С����Ƶ�һ��������Ϸ�ǣ�һ�����������P1(��3��9)��ʼ������ĺ�������������1�Ĺ��ɣ���������y��x2�������������õ���P2��P3��P4��P5��(��ͼ1��ʾ)����P1��P2��P3������P1H1��P2H2��P3H3��ֱ��x�ᣬ����ΪH1��H2��H3����S��P1P2P3��S����P1H1H3P3��S����P1H1H2P2��S����P2H2H3P3��![]() (9+1)��2��
(9+1)��2��![]() (9+4)��1��
(9+4)��1��![]() (4+1)��1������P1P2P3�����Ϊ1����
(4+1)��1������P1P2P3�����Ϊ1����
���⣺
(1)���ı���P1P2P3P4��P2P3P4P5�����(Ҫ��д������һ���ı�������������̣���һ��ֱ��д����)��
(2)�����ı���Pn��1PnPn+1Pn+2���������˵������(����ͼ2)��
(3)����������y��x2��Ϊ������y��x2+bx+c�������������䣬�����ı���Pn��1PnPn+1Pn+2�����(ֱ��д����)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O����ABC�����Բ��O����BC���ϣ���BAC��ƽ���߽���O�ڵ�D������BD��CD������D��BC��ƽ���ߣ���AB���ӳ����ཻ�ڵ�P��
��1����֤��PD�ǡ�O�����ߣ�
��2����֤����PBD�ס�DCA��
��3����AB=6��AC=8ʱ�����߶�PB�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ijС��ˮ����ˮ�ӵĺ�������ı���ABCD��DC��AB�����ӭˮ�µ��½���=30������֪��ˮ�µ��±�Ϊ1.2��1���Ӷ���DC��Ϊ2m���Ӹ�Ϊ6m����ӵ�AB�ij�Ϊ_____m��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬�ı���OABC�Ǿ��Σ�OA��x��ĸ������ϣ�OC��y����������ϣ�
![]() ��
��![]() ��
��![]() ��
��![]() ��
��
![]() ��ͼ1��������OABC�Ƶ�O˳ʱ�뷽����ת
��ͼ1��������OABC�Ƶ�O˳ʱ�뷽����ת![]() �õ�����
�õ�����![]() ������A�Ķ�Ӧ��
������A�Ķ�Ӧ��![]() ����BC����ʱ�����
����BC����ʱ�����![]() �����ꣻ
�����ꣻ
![]() ��ͼ��������OABC�Ƶ�O˳ʱ�뷽����
��ͼ��������OABC�Ƶ�O˳ʱ�뷽����![]() �õ�����
�õ�����![]() ������B�Ķ�Ӧ��
������B�Ķ�Ӧ��![]() ���������������ʱ�����
���������������ʱ�����![]() �����ꣻ
�����ꣻ
![]() ��
��![]() ��
��![]() ��
��![]() ����ͼ3�����
����ͼ3�����![]() ��BC���ڵ�E����
��BC���ڵ�E����![]() ����ֱ��д��
����ֱ��д��![]() ��ֵ��
��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����¥![]() �����Կ��������ij����壩�����ܶ��ǿտ���ˮƽ���森�������мס������ˣ��������ڷֱ�λ�ڵ�
�����Կ��������ij����壩�����ܶ��ǿտ���ˮƽ���森�������мס������ˣ��������ڷֱ�λ�ڵ�![]() �͵�
�͵�![]() ����
����![]() ��
��![]() ����
����![]() ���д����ϣ���
���д����ϣ���![]() ��
��![]() ����¥�ľ���ֱ�Ϊ
����¥�ľ���ֱ�Ϊ![]() ��
��![]() �ף�����֪
�ף�����֪![]() ��
��![]() �ף�
�ף�![]() ��
��![]() �ף����ڴ�¥�ڵ��ţ������Ҳ��ܿ����ף��������Ŵ�¥������ش����ߣ�ֱ�������ף��ױ��ֲ��������������ߵ���̾��볤Ϊ________�ף�
�ף����ڴ�¥�ڵ��ţ������Ҳ��ܿ����ף��������Ŵ�¥������ش����ߣ�ֱ�������ף��ױ��ֲ��������������ߵ���̾��볤Ϊ________�ף�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
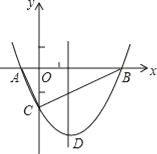
����Ŀ����ͼ��������y=![]() x2+bx��2��x�ύ��A��B���㣬��y�ύ��C�㣬��A��һ1��0����
x2+bx��2��x�ύ��A��B���㣬��y�ύ��C�㣬��A��һ1��0����
��1���������ߵĽ���ʽ������D�����ꣻ
��2���жϡ�ABC����״��֤����Ľ��ۣ�
��3����M�������߶Գ����ϵ�һ�����㣬����ACM�ܳ���Сʱ�����M�����꼰��ACM����С�ܳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=2x2+m����1�����㣨-2��y1���루3��y2���ڴ˶��κ�����ͼ���ϣ���y1_________y2��������������=����������������2����ͼ���˶��κ�����ͼ���㣨0��-4����������ABCD�Ķ���C��D��x���ϣ�A��Bǡ���ڶ��κ�����ͼ���ϣ���ͼ����Ӱ���ֵ����֮�ͣ�
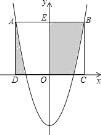
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com