
【题目】如图,D,E,F分别是OA,OB,OC的中点,下面的说法中:①△ABC与△DEF是位似图形;②△ABC与△DEF的相似比为1∶2;③△ABC与△DEF的周长之比为2∶1;④△ABC与△DEF的面积之比为4∶1.正确的是( )
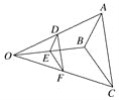
A. ①②③ B. ①③④ C. ①②④ D. ②③④
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,AD⊥BC,垂足为D.给出下列四个结论:①sinα=sinB;②sinβ=sinC;③sinB=cosC;④sinα=cosβ.其中正确的结论有_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,抛物线y=﹣x2+bx+c经过点A(﹣1,0)和C(0,3).(1)求抛物线的解析式;(2)在抛物线的对称轴上,是否存在点P,使PA+PC的值最小?如果存在,请求出点P的坐标,如果不存在,请说明理由;(3)设点M在抛物线的对称轴上,当△MAC是直角三角形时,求点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某民俗村为了维护消费者利益,限定村内所有商品的利润率不得超过![]() ,村内一商店以每件16元的价格购进一批商品,该商品每件售价定为x元,每天可卖出
,村内一商店以每件16元的价格购进一批商品,该商品每件售价定为x元,每天可卖出![]() 件,每天销售该商品所获得的利润为y元.
件,每天销售该商品所获得的利润为y元.
![]() 求y与x的函数关系式;
求y与x的函数关系式;
![]() 若每天销售该商品要获得280元的利润,每件商品的售价应定为多少元?
若每天销售该商品要获得280元的利润,每件商品的售价应定为多少元?
![]() 求商店每天销售该商品可获得的最大利润.
求商店每天销售该商品可获得的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,正三角形和正方形内接于同一个圆;如图②,正方形和正五边形内接于同一个圆;如图③,正五边形和正六边形内接于同一个圆;…;则对于图①来说,BD可以看作是正_____边形的边长;若正n边形和正(n+1)边形内接于同一个圆,连接与公共顶点相邻同侧两个不同正多边形的顶点可以看做是_____边形的边长.
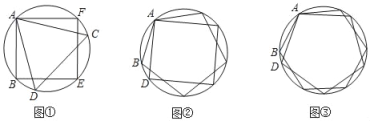
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中有两点A(﹣2,4)、B(2,4),若二次函数y=ax2﹣2ax﹣3a(a≠0)的图象与线段AB只有一个交点,则( )
A. a的值可以是![]() B. a的值可以是
B. a的值可以是![]()
C. a的值不可能是﹣1.2 D. a的值不可能是1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,图象经过B(﹣3,0)、C(0,3)两点,且与x轴交于点A.
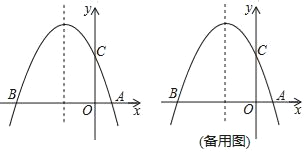
(1)求二次函数y=ax2+bx+c(a≠0)的表达式;
(2)在抛物线的对称轴上找一点M,使△ACM周长最短,求出点M的坐标;
(3)若点P为抛物线对称轴上的一个动点,直接写出使△BPC为直角三角形时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:Rt△ABC中,∠ACB=90°,点E为AB上一点,AC=AE=3,BC=4,过点A作AB的垂线交射线EC于点D,延长BC交AD于点F.
(1)求CF的长;
(2)求∠D的正切值.
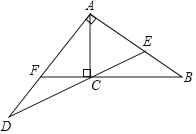
查看答案和解析>>
科目:初中数学 来源: 题型:
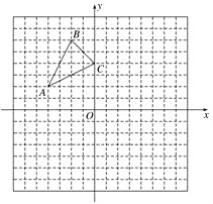
【题目】如图,已知A(-4,2),B(-2,6),C(0,4)是直角坐标系平面上三点.
(1)把△ABC向右平移4个单位再向下平移1个单位,得到△A1B1C1,画出平移后的图形;
(2)若△ABC内部有一点P(a,b),则平移后它的对应点P1的坐标为__________;
(3)以原点O为位似中心,将△ABC缩小为原来的一半,得到△A2B2C2,请在所给的坐标系中作出所有满足条件的图形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com