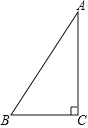
【题目】如图，△ABC 中，∠C＝90°，将△ABC 绕点 C 顺时针旋转 90°，得到△DEC（其中点 D、E 分别是 A、B 两点旋转后的对应点）．
(1)请画出旋转后的△DEC；
(2)试判断 DE 与 AB 的位置关系，并证明你的结论．
科目：初中数学 来源： 题型：
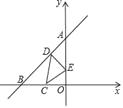
【题目】如图所示，直线 y=x+2 与两坐标轴分别交于A、B 两点，点 C 是 OB 的中点，D、E 分 别是直线 AB、y 轴上的动点，则△CDE 周长的最小值是________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，正方形
中，
是对角线
上一个动点，连结
，过
作
，
，
，
分别为垂足．
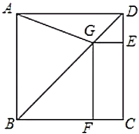
（1）求证：
；
（2）①写出
、
、三条线段满足的等量关系，并证明；②求当
，
时，
的长
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，在梯形ABCD中，AB∥CD，∠D=90°，AD=CD=2，点E在边AD上（不与点A、D重合），∠CEB=45°，EB与对角线AC相交于点F，设DE=x．
（1）用含x的代数式表示线段CF的长；
（2）如果把△CAE的周长记作C△CAE，△BAF的周长记作C△BAF，设
=y，求y关于x的函数关系式，并写出它的定义域；
（3）当∠ABE的正切值是
时，求AB的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
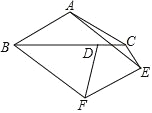
【题目】如图，在等腰△ABC 中，∠BAC＝120°，AB＝AC＝2
，点 D 在边 BC 上，CD＝
，将线段 CD 绕点 C 逆时针旋转α°（其中 0＜α≤360）到 CE，连接AE，以 AB，AE 为边作 ABFE，连接 DF，则 DF 的最大值为（ ）
A. 
+ B. 
+ C. 2+ D. +2
查看答案和解析>>
科目：初中数学 来源： 题型：
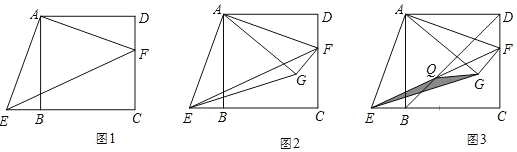
【题目】已知，在正方形 ABCD 中，AB＝5，点 F 是边 DC 上的一个动点，将△ADF 绕点 A 顺时针旋转 90°至△ABE，点 F 的对应点 E 落在 CB 的延长线上，连接 EF．
(1)如图 1，求证：∠DAF+∠FEC＝∠AEF；
(2)将△ADF 沿 AF 翻折至△AGF，连接 EG．
①如图 2，若 DF＝2，求 EG 的长；
②如图 3，连接 BD 交 EF 于点 Q，连接 GQ，则 S△QEG 的最大值为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
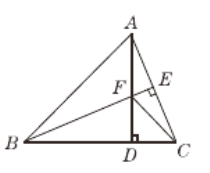
【题目】如图，在△ABC中，AB＝BC，BE⊥AC于点E，AD⊥BC于点D，∠BAD＝45°，AD与BE交于点F，连接CF.
（1）求证△ACD≌△BFD
（2）求证：BF＝2AE；
（3）若CD＝
，求AD的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
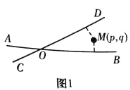
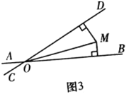
【题目】定义：如图1，平面上两条直线AB、CD相交于点O，对于平面内任意一点M，点M到直线AB、CD的距离分别为p、q，则称有序实数对(p，q)是点M的“距离坐标”，根据上述定义，“距离坐标”为（0，0）的点有1个，即点O．
（1）“距离坐标”为1，0的点有 个；
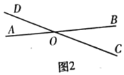
（2）如图2，若点M在过点O且与直线AB垂直的直线l上时，点M的“距离坐标”为p，q，且BOD 150，请写出p、q的关系式并证明；
（3）如图3，点M的“距离坐标”为
，且DOB 30，求OM的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
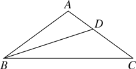
【题目】如图，在△ABC中，AB＝AC，∠A＝108°，BD平分∠ABC交AC于点D．
（1）填空：∠DBC=_________度；
（2）猜想：BC、AB、CD三者数量关系_____________________；
（3）证明你的猜想．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
