
【题目】如图,正方形![]() 中,
中,![]() 是对角线
是对角线![]() 上一个动点,连结
上一个动点,连结![]() ,过
,过![]() 作
作![]() ,
,![]() ,
,
![]() ,
,![]() 分别为垂足.
分别为垂足.
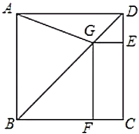
(1)求证:![]() ;
;
(2)①写出![]() 、
、![]() 、
、![]() 三条线段满足的等量关系,并证明;②求当
三条线段满足的等量关系,并证明;②求当![]() ,
,![]() 时,
时,![]() 的长
的长
【答案】(1)见解析;(2)①GE2+GF2=AG2,证明见解析;②![]() 的长为
的长为![]() 或
或![]() .
.
【解析】
(1)根据正方形的性质得出△DGE和△BGF是等腰直角三角形,可得GE=![]() DG,GF=
DG,GF=![]() BG,结合AB=
BG,结合AB=![]() BD即可得出结论;
BD即可得出结论;
(2)①连接CG,由SAS证明△ABG≌△CBG,得出AG=CG,证出四边形EGFC是矩形,得出CE=GF,由勾股定理即可得出GE2+GF2=AG2;
②设GE=CF=x,则GF=BF=6x,由①中结论得出方程求出CF=1或CF=5,再分情况讨论,由勾股定理求出BG即可.
解:(1)∵四边形ABCD为正方形,
∴∠BCD=90°,∠ABD=∠CDB=∠CBD=45°,AB=BC=CD,
∴△ABD是等腰直角三角形,
∴AB=![]() BD,
BD,
∵GE⊥CD,GF⊥BC,
∴△DGE和△BGF是等腰直角三角形,
∴GE=![]() DG,GF=
DG,GF=![]() BG,
BG,
∴GE+GF=![]() (DG+BG)=
(DG+BG)=![]() BD,
BD,
∴GE+GF=AB;
(2)①GE2+GF2=AG2,
证明:连接CG,如图所示:
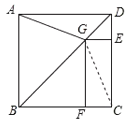
在△ABG和△CBG中,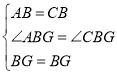 ,
,
∴△ABG≌△CBG(SAS),
∴AG=CG,
∵GE⊥CD,GF⊥BC,∠BCD=90°,
∴四边形EGFC是矩形,
∴CE=GF,
∵GE2+CE2=CG2,
∴GE2+GF2=AG2;
②设GE=CF=x,则GF=BF=6x,
∵GE2+GF2=AG2,
∴![]() ,
,
解得:x=1或x=5,
当x=1时,则BFGF=5,
∴BG=![]() ,
,
当x=5时,则BF=GF=1,
∴BG=![]() ,
,
综上,![]() 的长为
的长为![]() 或
或![]() .
.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
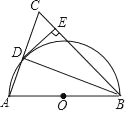
【题目】如图,在△ABC中,BA=BC,以AB为直径作⊙O,交AC于点D,连接DB,过点D作DE⊥BC,垂足为E.
(1)求证:AD=CD.
(2)求证:DE为⊙O的切线.
(3)若∠C=60°,DE=![]() ,求⊙O半径的长.
,求⊙O半径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数 y=ax2+bx+c(a≠0)的图象与 y 轴交于点(0,﹣2),且过点 A(﹣1,1)和 B(4,6).
(1)求二次函数的解析式,并写出其图象的顶点坐标;
(2)当 2≤x≤5 时,求二次函数的函数值 y 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,给出下列结论:
①b2=4ac;②abc>0;③a>c;④4a﹣2b+c>0,其中正确的个数有( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
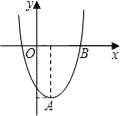
【题目】在直角坐标平面内,二次函数图象的顶点为A(1,﹣4),且过点B(3,0).
(1)求该二次函数的解析式;
(2)将该二次函数图象向右平移几个单位,可使平移后所得图象经过坐标原点?并直接写出平移后所得图象与x轴的另一个交点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司营销A,B两种产品,根据市场调研,发现如下信息:
信息1:销售A种产品所获利润y(万元)与所售产品x(吨)之间存在二次函数关系![]() 。
。
当x=1时,y=1.4;当x=3时,y=3.6。
信息2:销售B种产品所获利润y(万元)与所售产品x(吨)之间存在正比例函数关系![]() 。
。
根据以上信息,解答下列问题:
(1)求二次函数解析式;
(2)该公司准备购进A,B两种产品共10吨,请设计一个营销方案,使销售A,B两种产品获得的利润之和最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
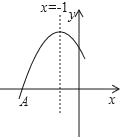
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为直线x=﹣1,给出以下结论,①ab<0,②b2﹣4ac>0,③4b+c<0,④若B(﹣![]() ,y1)、C(﹣
,y1)、C(﹣![]() ,y2)为函数图象上的两点,则y1>y2,⑤当﹣3≤x≤1时,y≥0,其中正确的结论是( )
,y2)为函数图象上的两点,则y1>y2,⑤当﹣3≤x≤1时,y≥0,其中正确的结论是( )
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
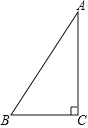
【题目】如图,△ABC 中,∠C=90°,将△ABC 绕点 C 顺时针旋转 90°,得到△DEC(其中点 D、E 分别是 A、B 两点旋转后的对应点).
(1)请画出旋转后的△DEC;
(2)试判断 DE 与 AB 的位置关系,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com