
分析:首先设点O是△APQ的外接圆的圆心,连接OP,OQ,作OH⊥PQ于点H,过点A作AD⊥BC于点D,由垂径定理与圆周角定理易得PQ=2OA•sin∠BAC,然后由当AD是直径时,即OA=

AD时,PQ最小,则可求得AD的长与sin∠BAC的值,则可求得答案.
解答:
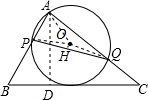
解:如图,设点O是△APQ的外接圆的圆心,连接OP,OQ,作OH⊥PQ于点H,过点A作AD⊥BC于点D,
∴PH=QH=

PQ,
∵OP=OQ,
∴∠POH=

∠POQ,
∵∠POQ=2∠BAC,
∴∠POH=∠BAC,
在Rt△POH中,PH=OP•sin∠POH=OA•sin∠BAC,
∴PQ=2OA•sin∠BAC,
即当OA最小时,PQ最小,
∵当AD是直径时,即OA=

AD时,PQ最小,
设BD=x,则CD=8-x,
∵在Rt△ABD中,AD
2=AB
2-AD
2,
在Rt△ACD中,AD
2=AC
2-CD
2,
∴25-x
2=49-(8-x)
2,
解得:x=

,
∴AD=

=

,
∴OA=
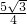
,
设AC边上的高为h,
则AC•h=BC•AD,
∴h=

=
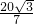
,
∴sin∠BAC=
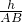
=
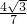
,
∴PQ=2OA•sin∠BAC=2×
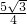
×
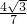
=

.
故答案为:

.
点评:此题考查了切线的性质、三角形外接圆的性质、勾股定理以及三角函数等知识.此题难度较大,注意掌握辅助线的作法,注意数形结合思想与方程思想的应用.

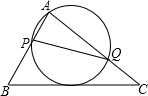 如图,在△ABC中,已知AB=5,BC=8,AC=7,动点P、Q分别在边AB、AC上,使△APQ的外接圆与BC相切,则线段PQ的最小值等于________.
如图,在△ABC中,已知AB=5,BC=8,AC=7,动点P、Q分别在边AB、AC上,使△APQ的外接圆与BC相切,则线段PQ的最小值等于________.
 AD时,PQ最小,则可求得AD的长与sin∠BAC的值,则可求得答案.
AD时,PQ最小,则可求得AD的长与sin∠BAC的值,则可求得答案. 解:如图,设点O是△APQ的外接圆的圆心,连接OP,OQ,作OH⊥PQ于点H,过点A作AD⊥BC于点D,
解:如图,设点O是△APQ的外接圆的圆心,连接OP,OQ,作OH⊥PQ于点H,过点A作AD⊥BC于点D, PQ,
PQ, ∠POQ,
∠POQ, AD时,PQ最小,
AD时,PQ最小, ,
, =
= ,
,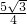 ,
, =
=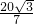 ,
,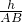 =
=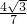 ,
,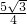 ×
×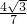 =
= .
. .
.

 轻松暑假总复习系列答案
轻松暑假总复习系列答案 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为