
【题目】如图,四边形ABCD中,对角线AC,BD相交于点O,点E,F分别在线段OA,OC上,且OB=OD,∠1=∠2,AE=CF.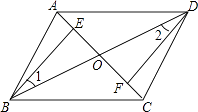
(1)证明:△BEO≌△DFO;
(2)证明:四边形ABCD是平行四边形.
【答案】
(1)证明:∵∠EOB与∠FOD是对顶角,
∴∠EOB=∠FOD,
在△BEO和△DFO中 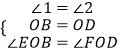
∴△BEO≌△DFO(ASA)
(2)证明:由(1)可知△BEO≌△DFO,
∴OE=OF,
∵AE=CF,
∴OA=OC,
∵OB=OD,
∴四边形ABCD为平行四边形.
【解析】(1)利用ASA易证出△BEO≌△DFO;
(2)由(1)中△BEO≌△DFO可得OE=OF。进而可得OA=OC,利用对角线互相平分的四边形是平行四边形可以证出结论.
【考点精析】本题主要考查了平行四边形的判定的相关知识点,需要掌握两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形才能正确解答此题.


科目:初中数学 来源: 题型:
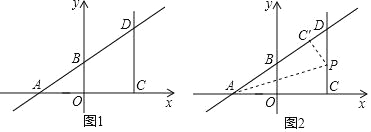
【题目】已知:如图1,在平面直角坐标系中,一次函数y=![]() x+3交x轴于点A,交y轴于点B,点C是点A关于y轴对称的点,过点C作y轴平行的射线CD,交直线AB与点D,点P是射线CD上的一个动点.
x+3交x轴于点A,交y轴于点B,点C是点A关于y轴对称的点,过点C作y轴平行的射线CD,交直线AB与点D,点P是射线CD上的一个动点.
(1)求点A,B的坐标.
(2)如图2,将△ACP沿着AP翻折,当点C的对应点C′落在直线AB上时,求点P的坐标.
(3)若直线OP与直线AD有交点,不妨设交点为Q(不与点D重合),连接CQ,是否存在点P,使得S△CPQ=2S△DPQ,若存在,请求出对应的点Q坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,直线l1:y=3x﹣2k与直线l2:y=x+k交点P的纵坐标为5,直线l1与直线l2与y轴分别交于A、B两点.
(1)求出点P的横坐标及k的值;
(2)求△PAB的面积;
(3)点M为直线l1上的一个动点,当△MAB面积与△PAB面积之比为2:3时,求此时的点M的坐标【1】

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小强作出边长为1的第1个等边△A1B1C1 , 计算器面积为S1 , 然后分别取△A1B1C1三边的中点A2、B2、C1 , 作出第2个等边△A2B2C2 , 计算其面积为S2 , 用同样的方法,作出第3个等边△A3B3C3 , 计算其面积为S3 , 按此规律进行下去,…,由此可得,第20个等边△A20B20C20的面积S20= . 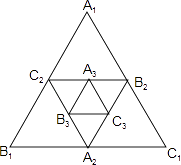
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是( )

A. 角的内部到角的两边的距离相等的点在角的平分线上
B. 角平分线上的点到这个角两边的距离相等
C. 三角形三条角平分线的交点到三条边的距离相等
D. 以上均不正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点D的对应点D′.
(1)根据特征画出平移后的△A′B′C′;
(2)利用网格的特征,画出AC边上的高BE并标出画法过程中的特征点;
(3)△A′B′C′的面积为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x+3与x轴相交于点A,与y轴相交于点B.
(1)求A,B两点的坐标;
(2)过B点作直线与x轴交于点P,若△ABP的面积为![]() ,试求点P的坐标.
,试求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】5.1劳动节,某校决定组织甲乙两队参加义务劳动,并购买队服.下面是服装厂给出的服装的价格表:
购买服装的套数 |
|
|
|
每套服装的价格 |
|
|
|
经调查:两个队共75人(甲队人数不少于40人),如果分别各自购买队服,两队共需花费5600元,请回答以下问题:
(1)如果甲、乙两队联合起来购买服装,那么比各自购买服装最多可以节省_________.
(2)甲、乙两队各有多少名学生?
(3)到了现场,因工作分配需要,临时决定从甲队抽调a人,从乙队抽调b人,组成丙队(要求从每队抽调的人数不少于10人),现已知重新组队后,甲队平均每人需植树1棵;乙队平均每人需植树4棵;丙队平均每人需植树6棵,甲乙丙三队共需植树265棵,请写出所有的抽调方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com