
【题目】已知:如图1,在平面直角坐标系中,一次函数y=![]() x+3交x轴于点A,交y轴于点B,点C是点A关于y轴对称的点,过点C作y轴平行的射线CD,交直线AB与点D,点P是射线CD上的一个动点.
x+3交x轴于点A,交y轴于点B,点C是点A关于y轴对称的点,过点C作y轴平行的射线CD,交直线AB与点D,点P是射线CD上的一个动点.
(1)求点A,B的坐标.
(2)如图2,将△ACP沿着AP翻折,当点C的对应点C′落在直线AB上时,求点P的坐标.
(3)若直线OP与直线AD有交点,不妨设交点为Q(不与点D重合),连接CQ,是否存在点P,使得S△CPQ=2S△DPQ,若存在,请求出对应的点Q坐标;若不存在,请说明理由.
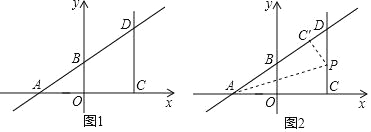
【答案】(1)A(﹣4,0),B(0,3);(2)P(4,![]() );(3)满足条件的点Q(12,12)或(
);(3)满足条件的点Q(12,12)或(![]() ,4).
,4).
【解析】
令x=0,y=0即可求出A,B坐标.
因为点C是点A关于y轴对称的点,求得C坐标,因为CD⊥x轴,所以求得D坐标,由折叠知,AC'=AC,所以C'D=AD﹣AC',设PC=a,在Rt△DC'P中通过勾股定理求得a值,即可求得P点坐标.
在S△CPQ=2S△DPQ情况下分类讨论P点坐标即可求解.
解:(1)令x=0,则y=3,
∴B(0,3),
令y=0,则![]() x+3=0,
x+3=0,
∴x=﹣4,
∴A(﹣4,0);
(2)∵点C是点A关于y轴对称的点,
∴C(4,0),
∵CD⊥x轴,
∴x=4时,y=6,∴D(4,6),
∴AC=8,CD=6,AD=10,
由折叠知,AC'=AC=8,
∴C'D=AD﹣AC'=2,
设PC=a,
∴PC'=a,DP=6﹣a,
在Rt△DC'P中,a2+4=(6﹣a)2,
∴a=![]() ,
,
∴P(4,![]() );
);
(3)设P(4,m),
∴CP=m,DP=|m﹣6|,
∵S△CPQ=2S△DPQ,
∴CP=2PD,
∴2|m﹣6|=m,
∴m=4或m=12,
∴P(4,4)或P(4,12),
∵直线AB的解析式为y=![]() x+3①,
x+3①,
当P(4,4)时,直线OP的解析式为y=x②,
联立①②解得,x=12,y=12,
∴Q(12,12),
当P(4,12)时,直线OP解析式为y=3x③,
联立①③解得,x=![]() ,y=4,
,y=4,
∴Q(![]() ,4),
,4),
即:满足条件的点Q(12,12)或(![]() ,4).
,4).


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,PM、QN分别是AB、AC的垂直平分线,∠BAC=100°那么∠PAQ等于( )

A. 50° B. 40° C. 30° D. 20°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市为庆祝开业举办大酬宾抽奖活动,凡在开业当天进店购物的顾客,都能获得一次抽奖的机会,抽奖规则如下:在一个不透明的盒子里装有分别标有数字1、2、3、4的4个小球,它们的形状、大小、质地完全相同,顾客先从盒子里随机取出一个小球,记下小球上标有的数字,然后把小球放回盒子并搅拌均匀,再从盒子中随机取出一个小球,记下小球上标有的数字,并计算两次记下的数字之和,若两次所得的数字之和为8,则可获得50元代金券一张;若所得的数字之和为6,则可获得30元代金券一张;若所得的数字之和为5,则可获得15元代金券一张;其他情况都不中奖.
(1)请用列表或树状图(树状图也称树形图)的方法(选其中一种即可),把抽奖一次可能出现的结果表示出来;
(2)假如你参加了该超市开业当天的一次抽奖活动,求能中奖的概率P.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A,B在数轴上的位置如图所示,其对应的数分别是a和b,对于以下结论:甲:b﹣a<0;乙:a+b>0;丙:|a|<|b|;丁:ab>0,其中正确的是( )![]()
A.甲、乙
B.丙、丁
C.甲、丙
D.乙、丁
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在平面直角坐标系中,O为坐标原点,四边形OABC是长方形,点A、C、D的坐标分别为A(9,0)、C(0,4),D(5,0),点P从点O出发,以每秒1个单位长度的速度沿O→C→B→A运动,点P的运动时间为t秒.则当t=____秒时,△ODP是腰长为5的等腰三角形?
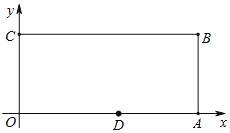
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,解答下面的问题:
我们知道方程![]() 有无数个解,但在实际生活中我们往往只需求出其
有无数个解,但在实际生活中我们往往只需求出其
正整数解.
例:由![]() ,得:
,得:![]() ,(x、y为正整数)
,(x、y为正整数)
∴![]() ,则有
,则有![]() .又
.又![]() 为正整数,则
为正整数,则![]() 为正整数.由2与3互质,可知:x为3的倍数,从而x=3,代入
为正整数.由2与3互质,可知:x为3的倍数,从而x=3,代入![]() ∴2x+3y=12的正整数解为
∴2x+3y=12的正整数解为![]()
问题:
(1)请你写出方程![]() 的一组正整数解: .
的一组正整数解: .
(2)若![]() 为自然数,则满足条件的x值为 .
为自然数,则满足条件的x值为 .
(3)七年级某班为了奖励学习进步的学生,购买了单价为3元的笔记本与单价为5元的钢笔两种奖品,共花费35元,问有几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,我们把横、纵坐标都是整数的点叫做整点.已知点A(0,4),点B是x轴正半轴上的整点,记△AOB内部(不包括边界)的整点个数为m.当点B的横坐标为4时,m的值是_____.当点B的横坐标为4n(n为正整数)时,m=_____(用含n的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,对角线AC,BD相交于点O,点E,F分别在线段OA,OC上,且OB=OD,∠1=∠2,AE=CF.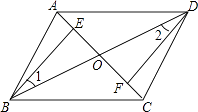
(1)证明:△BEO≌△DFO;
(2)证明:四边形ABCD是平行四边形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com