练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】点A，B在数轴上的位置如图所示，其对应的数分别是a和b，对于以下结论：甲：b﹣a＜0；乙：a+b＞0；丙：|a|＜|b|；丁：ab＞0，其中正确的是（ ）

    A.甲、乙
    B.丙、丁
    C.甲、丙
    D.乙、丁

    【答案】C
    【解析】∵b＜a，

    ∴b﹣a＜0；

    ∵b＜﹣3，0＜a＜3，

    ∴a+b＜0；

    ∵b＜﹣3，0＜a＜3，

    ∴|b|＞3，|a|＜3，

    ∴|a|＜|b|；

    ∵b＜0，a＞0，

    ∴ab＜0，

    ∴正确的是：甲、丙．

    所以答案是：C．

    【考点精析】认真审题，首先需要了解数轴(数轴是规定了原点、正方向、单位长度的一条直线)，还要掌握绝对值(正数的绝对值是其本身，0的绝对值是0，负数的绝对值是它的相反数；注意：绝对值的意义是数轴上表示某数的点离开原点的距离)的相关知识才是答题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，Rt△ABC中，AB⊥BC，AB=6，BC=4，P是△ABC内部的一个动点，且满足∠PAB=∠PBC，则线段CP长的最小值为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

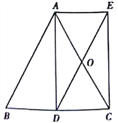
    【题目】如图，AD是等腰△ABC底边BC上的高，点O是AC中点，延长DO到E

    使AE∥BC，连接AE。

    （1）求证：四边形ADCE是矩形；

    （2）①若AB=17，BC=16，则四边形ADCE的面积＝ ；

    ②若AB=10，则BC＝ 时，四边形ADCE是正方形。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，河的两岸l1与l2相互平行，A，B是l1上的两点，C，D是l2上的两点，某人在点A处测得∠CAB=90°，∠DAB=30°，再沿AB方向前进20米到达点E（点E在线段AB上），测得∠DEB=60°，求C、D两点间的距离．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，已知抛物线y=﹣ x2﹣ x+c与x轴相交于A、B两点（B点在A点的左侧），与y轴相交于C点，且AB=10．

    （1）求这条抛物线的解析式；
    （2）如图2，D点在x轴上，且在A点的右侧，E点为抛物线上第二象限内的点，连接ED交抛物线于第二象限内的另外一点F，点E到y轴的距离与点F到y轴的距离之比为3：1，已知tan∠BDE= ，求点E的坐标；
    （3）如图3，在（2）的条件下，点G由B出发，沿x轴负方向运动，连接EG，点H在线段EG上，连接DH，∠EDH=∠EGB，过点E作EK⊥DH，与抛物线相应点E，若EK=EG，求点K的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知AB∥CD，∠A＝40°．点P是射线AB上一动点(与点A不重合)，CE、CF分别平分∠ACP和∠DCP交射线AB于点E、F．

    (1)求∠ECF的度数；

    (2)随着点P的运动，∠APC与∠AFC之间的数量关系是否改变？若不改变，请求出此数量关系；若改变，请说明理由；

    (3)当∠AEC＝∠ACF时，求∠APC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

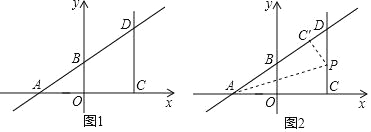
    【题目】已知：如图1，在平面直角坐标系中，一次函数y＝x+3交x轴于点A，交y轴于点B，点C是点A关于y轴对称的点，过点C作y轴平行的射线CD，交直线AB与点D，点P是射线CD上的一个动点．

    (1)求点A，B的坐标．

    (2)如图2，将△ACP沿着AP翻折，当点C的对应点C′落在直线AB上时，求点P的坐标．

    (3)若直线OP与直线AD有交点，不妨设交点为Q(不与点D重合)，连接CQ，是否存在点P，使得S△CPQ＝2S△DPQ，若存在，请求出对应的点Q坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】假期，某校为了勤工俭学,要完成整个A小区的绿化工作，开始由七年级单独工作了4天，完成整个绿化工作的三分之一，这时九年级也参加工作，两个年级又共同工作了2天，才全部完成整个绿化工作，则由九年级单独完成整个绿化工作需要____天.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，小强作出边长为1的第1个等边△A1B1C1 ， 计算器面积为S1 ， 然后分别取△A1B1C1三边的中点A2、B2、C1 ， 作出第2个等边△A2B2C2 ， 计算其面积为S2 ， 用同样的方法，作出第3个等边△A3B3C3 ， 计算其面积为S3 ， 按此规律进行下去，…，由此可得，第20个等边△A20B20C20的面积S20= ．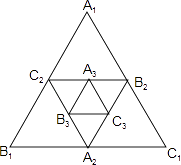

    查看答案和解析>>

    同步练习册答案