
【题目】如图1,已知抛物线y=﹣ ![]() x2﹣
x2﹣ ![]() x+c与x轴相交于A、B两点(B点在A点的左侧),与y轴相交于C点,且AB=10.
x+c与x轴相交于A、B两点(B点在A点的左侧),与y轴相交于C点,且AB=10.
(1)求这条抛物线的解析式;
(2)如图2,D点在x轴上,且在A点的右侧,E点为抛物线上第二象限内的点,连接ED交抛物线于第二象限内的另外一点F,点E到y轴的距离与点F到y轴的距离之比为3:1,已知tan∠BDE= ![]() ,求点E的坐标;
,求点E的坐标;
(3)如图3,在(2)的条件下,点G由B出发,沿x轴负方向运动,连接EG,点H在线段EG上,连接DH,∠EDH=∠EGB,过点E作EK⊥DH,与抛物线相应点E,若EK=EG,求点K的坐标.
【答案】
(1)解:由y=﹣ ![]() x2﹣
x2﹣ ![]() x+c,
x+c,
可得对称轴为x=﹣4
∵AB=10,
∴点A的坐标为(1,0),
∴ ![]() ,
,
∴c=3
∴抛物线的解析式为y=﹣ ![]() +3.
+3.
(2)解:如图2,作EM⊥x轴,垂足为点M,FN⊥x轴,垂足为点N,FT⊥EM,垂足为点T.
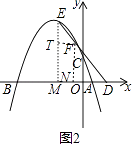
∴∠TMN=∠FNM=∠MTF=90°,
∴四边形FTMN为矩形,
∴EM∥FN,FT∥BD.
∴∠BDE=∠EFT,
∵tan∠BDE= ![]() ,
,
∴tan∠EFT= ![]() ,
,
设E(﹣3m,yE),F(﹣m,yF)
∴ ![]()
∵y=﹣ ![]() +3过点E、F,
+3过点E、F,
则yE﹣yF= ![]() =(﹣3m2+8m+3)﹣(﹣
=(﹣3m2+8m+3)﹣(﹣ ![]() +3),
+3),
解得m=0(舍去)或m=1,
当m=1时,﹣3m=﹣3,
∴ ![]() =8.
=8.
∴E(﹣3,8)
(3)解:如图3,作EM⊥x轴,垂足为点M,过点K作KR⊥ED,与ED相交于点R,与x轴相交于点Q.
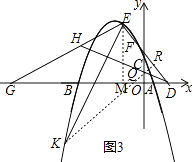
∵∠KER+∠EDH=90°,∠EGM+∠GEM=90°,∠EDH=∠EGM,
∴∠KER=∠GEM,
在△EGM和△EKR中,
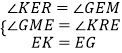
∴△EGM≌△EKR,
∴EM=ER=8,
∵tan∠BDE= ![]() .
.
∴ED=10,
∴DR=2,
∴DQ= ![]()
∴Q(﹣ ![]() ,0),
,0),
可求R( ![]() ,
, ![]() )
)
∴直线RQ的解析式为:y= ![]() .
.
设点K的坐标为(x, ![]() )代入抛物线解析式可得x=﹣11
)代入抛物线解析式可得x=﹣11
∴K(﹣11,﹣8).
【解析】(1)利用抛物线的轴对称性,求出对称轴,结合AB=10,求出A点坐标代入即可;(2)设出E的横坐标,表示 出E、F的纵坐标,利用tan∠BDE的定义构建关于m的方程,求出E的坐标;(3)通过作垂线构造出全等三角形,即△EGM≌△EKR,求出直线RQ解析式,解出二者联立的方程组, 即可求出其与抛物线交点坐标.


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,点E在线段CB的延长线上,连接DE交AB于点F,∠AED=2∠CED,点G是DF的中点,若BE=2,DF=8,则AB的长为______ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点P(1,0).点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位至点P3,第4次向右跳动3个单位至点P4,第5次又向上跳动1个单位至点P5,第6次向左跳动4个单位至点P6,…….照此规律,点P第100次跳动至点P100的坐标是( )

A. (-26,50) B. (-25,50) C. (26,50) D. (25,50)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市为庆祝开业举办大酬宾抽奖活动,凡在开业当天进店购物的顾客,都能获得一次抽奖的机会,抽奖规则如下:在一个不透明的盒子里装有分别标有数字1、2、3、4的4个小球,它们的形状、大小、质地完全相同,顾客先从盒子里随机取出一个小球,记下小球上标有的数字,然后把小球放回盒子并搅拌均匀,再从盒子中随机取出一个小球,记下小球上标有的数字,并计算两次记下的数字之和,若两次所得的数字之和为8,则可获得50元代金券一张;若所得的数字之和为6,则可获得30元代金券一张;若所得的数字之和为5,则可获得15元代金券一张;其他情况都不中奖.
(1)请用列表或树状图(树状图也称树形图)的方法(选其中一种即可),把抽奖一次可能出现的结果表示出来;
(2)假如你参加了该超市开业当天的一次抽奖活动,求能中奖的概率P.
查看答案和解析>>
科目:初中数学 来源: 题型:
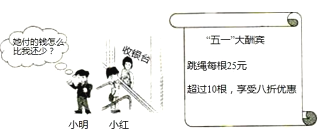
【题目】试根据图中信息,解答下列问题:
(1)购买8根跳绳需________元,购买14根跳绳需________元;
(2)小红比小明多买2根,付款时小红反而比小明少5元,你认为有这种可能吗?若有,请求小红购买跳绳的根数;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A,B在数轴上的位置如图所示,其对应的数分别是a和b,对于以下结论:甲:b﹣a<0;乙:a+b>0;丙:|a|<|b|;丁:ab>0,其中正确的是( )![]()
A.甲、乙
B.丙、丁
C.甲、丙
D.乙、丁
查看答案和解析>>
科目:初中数学 来源: 题型:
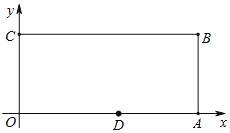
【题目】如图,已知在平面直角坐标系中,O为坐标原点,四边形OABC是长方形,点A、C、D的坐标分别为A(9,0)、C(0,4),D(5,0),点P从点O出发,以每秒1个单位长度的速度沿O→C→B→A运动,点P的运动时间为t秒.则当t=____秒时,△ODP是腰长为5的等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,解答下面的问题:
我们知道方程![]() 有无数个解,但在实际生活中我们往往只需求出其
有无数个解,但在实际生活中我们往往只需求出其
正整数解.
例:由![]() ,得:
,得:![]() ,(x、y为正整数)
,(x、y为正整数)
∴![]() ,则有
,则有![]() .又
.又![]() 为正整数,则
为正整数,则![]() 为正整数.由2与3互质,可知:x为3的倍数,从而x=3,代入
为正整数.由2与3互质,可知:x为3的倍数,从而x=3,代入![]() ∴2x+3y=12的正整数解为
∴2x+3y=12的正整数解为![]()
问题:
(1)请你写出方程![]() 的一组正整数解: .
的一组正整数解: .
(2)若![]() 为自然数,则满足条件的x值为 .
为自然数,则满足条件的x值为 .
(3)七年级某班为了奖励学习进步的学生,购买了单价为3元的笔记本与单价为5元的钢笔两种奖品,共花费35元,问有几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若我们规定三角“![]() ”表示为:abc;方框“
”表示为:abc;方框“![]() ”表示为:(xm+yn).例如:
”表示为:(xm+yn).例如:![]() =1×19×3÷(24+31)=3.请根据这个规定解答下列问题:
=1×19×3÷(24+31)=3.请根据这个规定解答下列问题:
(1)计算:![]() = ______ ;
= ______ ;
(2)代数式 为完全平方式,则k= ______ ;
为完全平方式,则k= ______ ;
(3)解方程:![]() =6x2+7.
=6x2+7.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com