
【题目】如图,四边形ABCD是矩形,点E在线段CB的延长线上,连接DE交AB于点F,∠AED=2∠CED,点G是DF的中点,若BE=2,DF=8,则AB的长为______ .

 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
【题目】已知O为直线AB上的一点,∠COE是直角,OF平分∠AOE.
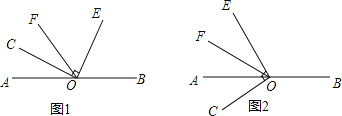
(1)如图1,若∠COF=34°,则∠BOE=______;
(2)如图1,若∠BOE=80°,则∠COF=______;
(3)若∠COF=m°,则∠BOE=______度;∠BOE与∠COF的数量关系为______.
(4)当∠COE绕点O逆时针旋转到如图2的位置时,(3)中∠BOE与∠COF的数量关系是否仍然成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB<BC,E为CD边的中点,将△ADE绕点E顺时针旋转180°,点D的对应点为C,点A的对应点为F,过点E作ME⊥AF交BC于点M,连接AM、BD交于点N,现有下列结论:
①AM=AD+MC;②AM=DE+BM;③DE2=ADCM;④点N为△ABM的外心.其中正确的个数为( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条公路上顺次有A、B、C三地,甲、乙两车同时从A地出发,分别匀速前往B地,C地,甲车到达B地停留一段时间后原速原路返回,乙车到达C地后立即原速原路返回,乙车比甲车早1小时返回A地,甲、乙两车各自行驶的路程y(千米)与时间x(时)(从两车出发时开始计时)之间的图象如图所示.
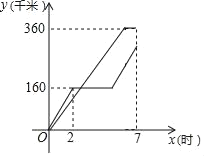
(1)在上述变化过程中,自变量是 ,因变量是 .
(2)乙车行驶的速度为 千米/小时;
(3)甲车到达B地停留了多久?B地与C地之间的距离为多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于点P(x,y),若点Q的坐标为(ax+y,x+ay),其中a为常数,则称点Q是点P的“a级关联点”例如,点P(1,4)的“3级美联点”为Q(3![]() +4,1+3
+4,1+3![]() ),即Q(7,13).
),即Q(7,13).
(1)已知点A(一2,6)的“![]() 级关联点”是点
级关联点”是点![]() ,求点
,求点![]() 的坐标。
的坐标。
(2)已知点M(m一1,2m)的“一3级关联点”M’位于y轴上.求点M’的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线y=﹣ ![]() x2﹣
x2﹣ ![]() x+c与x轴相交于A、B两点(B点在A点的左侧),与y轴相交于C点,且AB=10.
x+c与x轴相交于A、B两点(B点在A点的左侧),与y轴相交于C点,且AB=10.
(1)求这条抛物线的解析式;
(2)如图2,D点在x轴上,且在A点的右侧,E点为抛物线上第二象限内的点,连接ED交抛物线于第二象限内的另外一点F,点E到y轴的距离与点F到y轴的距离之比为3:1,已知tan∠BDE= ![]() ,求点E的坐标;
,求点E的坐标;
(3)如图3,在(2)的条件下,点G由B出发,沿x轴负方向运动,连接EG,点H在线段EG上,连接DH,∠EDH=∠EGB,过点E作EK⊥DH,与抛物线相应点E,若EK=EG,求点K的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com