Question

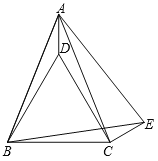
【题目】如图，在矩形ABCD中，AB＜BC，E为CD边的中点，将△ADE绕点E顺时针旋转180°，点D的对应点为C，点A的对应点为F，过点E作ME⊥AF交BC于点M，连接AM、BD交于点N，现有下列结论：

①AM=AD+MC；②AM=DE+BM；③DE2=ADCM；④点N为△ABM的外心．其中正确的个数为（　　）

A. 1个 B. 2个 C. 3个 D. 4个

Answer 1

【答案】B

【解析】解：∵E为CD边的中点，∴DE=CE，又∵∠D=∠ECF=90°，∠AED=∠FEC，∴△ADE≌△FCE，∴AD=CF，AE=FE，又∵ME⊥AF，∴ME垂直平分AF，∴AM=MF=MC+CF，∴AM=MC+AD，故①正确；

当AB=BC时，即四边形ABCD为正方形时，设DE=EC=1，BM=a，则AB=2，BF=4，AM=FM=4﹣a，在Rt△ABM中，22+a2=（4﹣a）2，解得a=1.5，即BM=1.5，∴由勾股定理可得AM=2.5，∴DE+BM=2.5=AM，又∵AB＜BC，∴AM=DE+BM不成立，故②错误；

∵ME⊥FF，EC⊥MF，∴EC2=CM×CF，又∵EC=DE，AD=CF，∴DE2=ADCM，故③正确；

∵∠ABM=90°，∴AM是△ABM的外接圆的直径，∵BM＜AD，∴当BM∥AD时， ＜1，∴N不是AM的中点，∴点N不是△ABM的外心，故④错误．

综上所述，正确的结论有2个，故选B．