
【题目】已知O为直线AB上的一点,∠COE是直角,OF平分∠AOE.
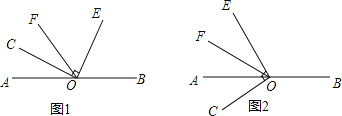
(1)如图1,若∠COF=34°,则∠BOE=______;
(2)如图1,若∠BOE=80°,则∠COF=______;
(3)若∠COF=m°,则∠BOE=______度;∠BOE与∠COF的数量关系为______.
(4)当∠COE绕点O逆时针旋转到如图2的位置时,(3)中∠BOE与∠COF的数量关系是否仍然成立?请说明理由.
【答案】(1)68° (2) 40° (3) 2m ∠BOE=2∠COF;(4)成立,理由见解析.
【解析】
(1)根据互余得到∠EOF=90°-34°,再由OF平分∠AOE,得到∠AOE=2∠EOF,然后根据邻补角的定义即可得到∠BOE;
(2)设∠COF=n°,根据互余得到∠EOF=90°-n°,再由OF平分∠AOE,得到∠AOE=2∠EOF=180°-2n°,然后根据邻补角的定义得到∠BOE=180°-(180°-2n°)=2n°=80°,于是得到结论;
(3)当∠COF=m°,根据互余得到∠EOF=90°-m°,再由OF平分∠AOE,得到∠AOE=2∠EOF=180°-2m°,然后根据邻补角的定义得到∠BOE=180°-(180°-2m°)=2m°,所以有∠BOE=2∠COF;
(4)同(3),可得到∠BOE=2∠COF.
解:(1)∵∠COE是直角,∠COF=34°,
∴∠EOF=90°-34°=56°,
∵OF平分∠AOE.
∴∠AOE=2∠EOF=112°,
∴∠BOE=180°-112°=68°;
(2)设∠COF=n°,
∴∠EOF=90°-n°,
∴∠AOE=2∠EOF=180°-2n°,
∴∠BOE=180°-(180°-2n°)=2n°=80°,
∴∠COF=40°;
(3)当∠COF=m°,
∴∠EOF=90°-m°,
∴∠AOE=2∠EOF=180°-2m°,
∴∠BOE=180°-(180°-2m°)=2m°,
∴∠BOE=2∠COF;
(4)∠BOE与∠COF的数量关系仍然成立.理由如下:
设∠COF=n°,
∵∠COE是直角,
∴∠EOF=90°-n°,
又∵OF平分∠AOE.
∴∠AOE=2∠EOF=180°-2n°,
∴∠BOE=180°-(180°-2n°)=2n°,
即∠BOE=2∠COF.
故答案为:(1)68° ;(2) 40° ;(3) 2m ,∠BOE=2∠COF ;(4)成立,理由见解析.


科目:初中数学 来源: 题型:
【题目】有5张边长为2的正方形纸片,4张边长分别为2、3的矩形纸片,6张边长为3的正方形纸片,从其中取出若干张纸片,且每种纸片至少取一张,把取出的这些纸片拼成一个正方形(原纸张进行无空隙、无重叠拼接),则拼成正方形的边长最大为 ( )
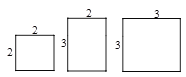
A. 6B. 7C. 8D. 9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售某种商品,原价560元.随着不同幅度的降价(元),日销售量(件)发生相应变化,关系如图所示:

(1)根据图像完成下表
降价/元 | 5 | 10 | 15 | |
日销售量/件 | 780 | 840 | 870 |
(2)售价为560元时,日销售量为多少件.
(3)如果该商场要求日销售量为1110件,该商品应降价多少元.
(4)设该商品的售价为![]() 元,日销售量为
元,日销售量为![]() 件,求
件,求![]() 与
与![]() 之间的关系式.
之间的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了测量被池塘隔开的A,B两点之间的距离,根据实际情况,作出如图所示图形,其中AB⊥BE,EF⊥BE,AF交BE于D,C在BD上.有四位同学分别测量出以下四组数据,根据所测数据不能求出A,B间距离的是( )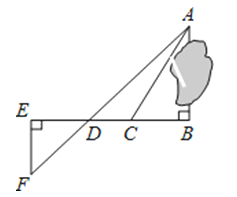
A.BC,∠ACB
B.DE,DC,BC
C.EF,DE,BD
D.CD,∠ACB,∠ADB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】赵爽弦图是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形,如图所示,若这四个全等直角三角形的两条直角边分别平行于x轴和y轴,大正方形的顶点B1、C1、C2、C3、…、Cn在直线y=﹣ ![]() x+
x+ ![]() 上,顶点D1、D2、D3、…、Dn在x轴上,则第n个阴影小正方形的面积为 .
上,顶点D1、D2、D3、…、Dn在x轴上,则第n个阴影小正方形的面积为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点D在反比例函数y= ![]() 的图象上,过点D作x轴的平行线交y轴于点B(0,3).过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC=
的图象上,过点D作x轴的平行线交y轴于点B(0,3).过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC= ![]() .
.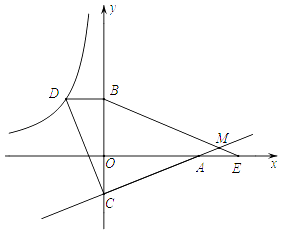
(1)求反比例函数y= ![]() 和直线y=kx+b的解析式;
和直线y=kx+b的解析式;
(2)连接CD,试判断线段AC与线段CD的关系,并说明理由;
(3)点E为x轴上点A右侧的一点,且AE=OC,连接BE交直线CA与点M,求∠BMC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个小组同时从甲地出发,匀速步行到乙地,甲乙两地相距7500米,第一组的步行速度是第二组的1.2倍,并且比第二组早15分钟到达乙地.设第二组的步行速度为x千米/小时,根据题意可列方程是( )
A.![]() ﹣
﹣ ![]() =15
=15
B.![]() ﹣
﹣ ![]() =
= ![]()
C.![]() ﹣
﹣ ![]() =15
=15
D.![]() ﹣
﹣ ![]() =
= ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,点E在线段CB的延长线上,连接DE交AB于点F,∠AED=2∠CED,点G是DF的中点,若BE=2,DF=8,则AB的长为______ .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com