
【题目】如图,已知点D在反比例函数y= ![]() 的图象上,过点D作x轴的平行线交y轴于点B(0,3).过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC=
的图象上,过点D作x轴的平行线交y轴于点B(0,3).过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC= ![]() .
.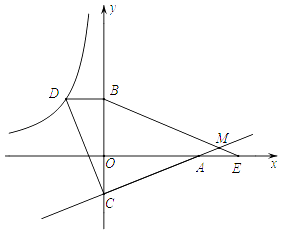
(1)求反比例函数y= ![]() 和直线y=kx+b的解析式;
和直线y=kx+b的解析式;
(2)连接CD,试判断线段AC与线段CD的关系,并说明理由;
(3)点E为x轴上点A右侧的一点,且AE=OC,连接BE交直线CA与点M,求∠BMC的度数.
【答案】
(1)解:∵A(5,0),
∴OA=5.
∵ ![]() ,
,
∴ ![]() ,解得OC=2,
,解得OC=2,
∴C(0,﹣2),
∴BD=OC=2,
∵B(0,3),BD∥x轴,
∴D(﹣2,3),
∴m=﹣2×3=﹣6,
∴ ![]() ,
,
设直线AC关系式为y=kx+b,
∵过A(5,0),C(0,﹣2),
∴ ![]() ,解得
,解得  ,
,
∴ ![]() ;
;
(2)解:∵B(0,3),C(0,﹣2),
∴BC=5=OA,
在△OAC和△BCD中

∴△OAC≌△BCD(SAS),
∴AC=CD,
∴∠OAC=∠BCD,
∴∠BCD+∠BCA=∠OAC+∠BCA=90°,
∴AC⊥CD;
(3)解:∠BMC=45°.
如图,连接AD,
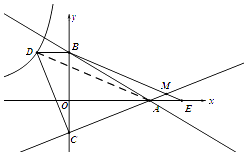
∵AE=OC,BD=OC,AE=BD,
∴BD∥x轴,
∴四边形AEBD为平行四边形,
∴AD∥BM,
∴∠BMC=∠DAC,
∵△OAC≌△BCD,
∴AC=CD,
∵AC⊥CD,
∴△ACD为等腰直角三角形,
∴∠BMC=∠DAC=45°.
【解析】(1)由正切定义可求C坐标,进而由BD=OC求出D坐标,求出 反比例函数解析式;由A、C求出直线解析式;(2)由条件可判定△OAC≌△BCD,得出AC=CD,∠OAC=∠BCD,进而AC⊥CD;(3) 由已知可得AE=OC,BD=OC,得出AE=BD,再加平行得四边形AEBD为平行四边形,推出 △OAC≌△BCD,∴AC=CD,∵AC⊥CD,∴△ACD为等腰直角三角形,∴∠BMC=∠DAC=45°.
【考点精析】本题主要考查了比例系数k的几何意义的相关知识点,需要掌握几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】计算:(1)∣—6∣+(![]() —3.14)0—(
—3.14)0—(![]() )-2+(—2)3 (2)(-a)3a2+(2a4)2÷a3.
)-2+(—2)3 (2)(-a)3a2+(2a4)2÷a3.
(3)![]() (4)(a-2b)(a+b)-3a(a+b)
(4)(a-2b)(a+b)-3a(a+b)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边△ABC外侧作直线AP,点B关于直线AP的对称点为D,连结BD,CD,其中CD交直线AP与点E.
(1)如图1,若∠PAB=30°,则∠ACE= ;
(2)如图2,若60°<∠PAB<120°,请补全图形,判断由线段AB,CE,ED可以构成一个含有多少度角的三角形,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知O为直线AB上的一点,∠COE是直角,OF平分∠AOE.
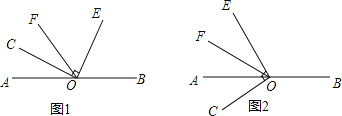
(1)如图1,若∠COF=34°,则∠BOE=______;
(2)如图1,若∠BOE=80°,则∠COF=______;
(3)若∠COF=m°,则∠BOE=______度;∠BOE与∠COF的数量关系为______.
(4)当∠COE绕点O逆时针旋转到如图2的位置时,(3)中∠BOE与∠COF的数量关系是否仍然成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某人到岛上去探宝,从A处登陆后先往东走4 km,又往北走1.5 km,遇到障碍后又往西走2 km,再折回向北走到4.5 km处往东一拐,仅走0.5 km就找到宝藏.问登陆点A与宝藏埋藏点B之间的距离是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的图形中,所有四边形都是正方形,所有的三角形都是直角三角形,其中最大正方形边长为7cm,设正方形A、B、C、D、E、F面积分别为SA、SB、SC、SD、SE、SF,则下列各式正确有()个.

① SA+SB+SC+SD=49;② SE+SF=49;③ SA+SB+SF=49;④ SC+SD+SE=4
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一电线杆AB的影子分别落在了地上和墙上.同一时刻,小明竖起1米高的直杆MN,量得其影长MF为0.5米,量得电线杆AB落在地上的影子BD长3米,落在墙上的影子CD的高为2米.你能利用小明测量的数据算出电线杆AB的高吗? 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条公路上顺次有A、B、C三地,甲、乙两车同时从A地出发,分别匀速前往B地,C地,甲车到达B地停留一段时间后原速原路返回,乙车到达C地后立即原速原路返回,乙车比甲车早1小时返回A地,甲、乙两车各自行驶的路程y(千米)与时间x(时)(从两车出发时开始计时)之间的图象如图所示.
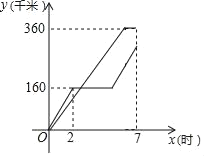
(1)在上述变化过程中,自变量是 ,因变量是 .
(2)乙车行驶的速度为 千米/小时;
(3)甲车到达B地停留了多久?B地与C地之间的距离为多少千米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com