
【题目】如图,一电线杆AB的影子分别落在了地上和墙上.同一时刻,小明竖起1米高的直杆MN,量得其影长MF为0.5米,量得电线杆AB落在地上的影子BD长3米,落在墙上的影子CD的高为2米.你能利用小明测量的数据算出电线杆AB的高吗? 
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】计算题:
(1)(﹣8)+3+10+(﹣2)
(2)(﹣2)×(﹣6)÷(﹣![]() )
)
(3)(﹣1)100×2+(﹣2)3÷4
(4)2(a﹣3b)+3(2b﹣3a)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了测量被池塘隔开的A,B两点之间的距离,根据实际情况,作出如图所示图形,其中AB⊥BE,EF⊥BE,AF交BE于D,C在BD上.有四位同学分别测量出以下四组数据,根据所测数据不能求出A,B间距离的是( )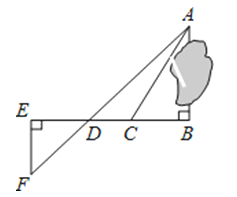
A.BC,∠ACB
B.DE,DC,BC
C.EF,DE,BD
D.CD,∠ACB,∠ADB
查看答案和解析>>
科目:初中数学 来源: 题型:
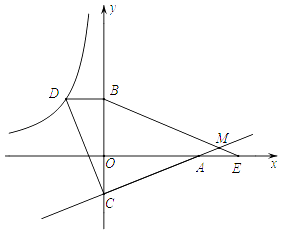
【题目】如图,已知点D在反比例函数y= ![]() 的图象上,过点D作x轴的平行线交y轴于点B(0,3).过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC=
的图象上,过点D作x轴的平行线交y轴于点B(0,3).过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC= ![]() .
.
(1)求反比例函数y= ![]() 和直线y=kx+b的解析式;
和直线y=kx+b的解析式;
(2)连接CD,试判断线段AC与线段CD的关系,并说明理由;
(3)点E为x轴上点A右侧的一点,且AE=OC,连接BE交直线CA与点M,求∠BMC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,CD⊥AB于D.
(1)图中有几个直角三角形;
(2)若AD=12,AC=13,则CD等于多少;
(3)若CD2=AD·DB, 求证:△ABC是直角三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个小组同时从甲地出发,匀速步行到乙地,甲乙两地相距7500米,第一组的步行速度是第二组的1.2倍,并且比第二组早15分钟到达乙地.设第二组的步行速度为x千米/小时,根据题意可列方程是( )
A.![]() ﹣
﹣ ![]() =15
=15
B.![]() ﹣
﹣ ![]() =
= ![]()
C.![]() ﹣
﹣ ![]() =15
=15
D.![]() ﹣
﹣ ![]() =
= ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆货车从百货大楼出发负责送货,向东走了4千米到达小明家,继续向东走了1.5千米到达小红家,然后向西走了8.5千米到达小刚家,最后返回百货大楼.

(1)以百货大楼为原点,向东为正方向,1个单位长度表示1千米,请你在数轴上标出小明、小红、小刚家的位置.(小明家用点A表示,小红家用点B表示,小刚家用点C表示)
(2)小明家与小刚家相距多远?
(3)若货车每千米耗油1.5升,那么这辆货车此次送货共耗油多少升
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,在△ABC中,AB=AC,分别以AB、BC为边作等边△ABE和等边△BCD,连结CE、AD.
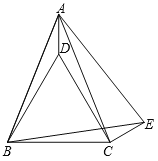
(1)求证:∠ACD=∠ABD;
(2)判断DC与CE的位置关系,并加以证明;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小正方形的边长均为1,四边形ABCD的四个顶点都在小正方形的顶点(小正方形的顶点叫格点)上,连接BD.

(1)利用格点在图中画出△ABD中AD边上的高,垂足为H.
(2)①画出将△ABD先向右平移2格,再向上平移2格得到的△A1B1D1;
②平移后,求线段AB扫过的部分所组成的封闭图形的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com