
【题目】如图,△ABC中,CD⊥AB于D.
(1)图中有几个直角三角形;
(2)若AD=12,AC=13,则CD等于多少;
(3)若CD2=AD·DB, 求证:△ABC是直角三角形.

【答案】(1)2;(2)5;(3)见解析.
【解析】
(1)根据CD⊥AB即可进行判断;
(2)利用勾股定理求解即可;
(3)根据勾股定理可得BD2=BC2﹣CD2,AD2=AC2﹣CD2,再利用完全平方公式(AD+BD)2=AD2+2AD·BD+BD2,代入整理,根据勾股定理的逆定理即可得证.
(1)∵CD⊥AB,
∴△ACD与△BCD都是直角三角形,
故图中有2个直角三角形;
(2)在Rt△ACD中,
CD=![]() =5;
=5;
(3)在Rt△ACD中,AD2=AC2﹣CD2,
在Rt△BCD中,BD2=BC2﹣CD2,
∵CD2=AD·DB,
∴(AD+BD)2=AD2+2AD·BD+BD2
= AC2﹣CD2+2 CD2+BC2﹣CD2
= AC2+ BC2=AB2,
则△ABC是直角三角形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某电器超市销售每台进价分别为200元,170元的A,B两种型号的电风扇,表中是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 1800元 |
第二周 | 4台 | 10台 | 3100元 |
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求A,B两种型号的电风扇的销售单价.
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,则A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
甲列车从A地开往B地,每小时行驶60千米,乙列车同时从B地开往A地,每小时行驶90千米.已知A,B两地相距200km.
(1)经过多长时间两车相遇;
(2)两车相遇的地方离A地多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某人到岛上去探宝,从A处登陆后先往东走4 km,又往北走1.5 km,遇到障碍后又往西走2 km,再折回向北走到4.5 km处往东一拐,仅走0.5 km就找到宝藏.问登陆点A与宝藏埋藏点B之间的距离是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
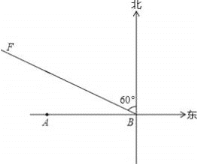
【题目】如图,A市气象站测得台风中心在A市正东方向300千米的B处,以10![]() 千米/时的速度向北偏西60°的BF方向移动,距台风中心200千米范围内是受台风影响的区域.
千米/时的速度向北偏西60°的BF方向移动,距台风中心200千米范围内是受台风影响的区域.
(1)A市是否会受到台风的影响?写出你的结论并给予说明;
(2)如果A市受这次台风影响,那么受台风影响的时间有多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一电线杆AB的影子分别落在了地上和墙上.同一时刻,小明竖起1米高的直杆MN,量得其影长MF为0.5米,量得电线杆AB落在地上的影子BD长3米,落在墙上的影子CD的高为2米.你能利用小明测量的数据算出电线杆AB的高吗? 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业新增了一个化工项目,为了节约资源,保护环境,该企业决定购买A、B两种型号的污水处理设备共8台,具体情况如下表:
A型 | B型 | |
价格(万元/台) | 12 | 10 |
月污水处理能力(吨/月) | 200 | 160 |
经预算,企业最多支出89万元购买设备,且要求月处理污水能力不低于1380吨.
(1)该企业有几种购买方案?
(2)哪种方案更省钱,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com