
【题目】某企业新增了一个化工项目,为了节约资源,保护环境,该企业决定购买A、B两种型号的污水处理设备共8台,具体情况如下表:
A型 | B型 | |
价格(万元/台) | 12 | 10 |
月污水处理能力(吨/月) | 200 | 160 |
经预算,企业最多支出89万元购买设备,且要求月处理污水能力不低于1380吨.
(1)该企业有几种购买方案?
(2)哪种方案更省钱,说明理由.
【答案】(1)有2种购买方案:第一种是购买3台A型污水处理设备,5台B型污水处理设备;
第二种是购买4台A型污水处理设备,4台B型污水处理设备;
(2)购买3台A型污水处理设备,5台B型污水处理设备更省钱.理由见解析
【解析】
试题(1)设购买污水处理设备A型号x台,则购买B型号(8﹣x)台,根据企业最多支出89万元购买设备,要求月处理污水能力不低于1380吨,列出不等式组,然后找出最合适的方案即可.(2)计算出每一方案的花费,通过比较即可得到答案.
试题解析:(1)、设购买污水处理设备A型号x台,则购买B型号(8﹣x)台, 根据题意,得
![]() , 解这个不等式组,得:2.5≤x≤4.5. ∵x是整数, ∴x=3或x=4.
, 解这个不等式组,得:2.5≤x≤4.5. ∵x是整数, ∴x=3或x=4.
当x=3时,8﹣x=5; 当x=4时,8﹣x=4.第二种是购买4台A型污水处理设备,4台B型污水处理设备;
(2)、当x=3时,购买资金为12×3+10×5=86(万元), 当x=4时,购买资金为12×4+10×4=88(万元).
因为88>86, 所以为了节约资金,应购污水处理设备A型号3台,B型号5台.


科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,点D在边BC上,∠ABC:∠ACB:∠ADB=1:2:3,⊙O是△ABD的外接圆.
(1)求证:AC是⊙O的切线;
(2)当BD是⊙O的直径时(如图2),求∠CAD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明同学用自制的直角三角形纸板EFG测量树的高度AB,他调整自己的位置,设法使斜边EG保持水平,并且边EF所在的直线经过点A.已知纸板的两条直角边EF=60cm,FG=30cm,测得小刚与树的水平距离BD=8m,边EG离地面的高度DE=1.6m,则树的高度AB等于( )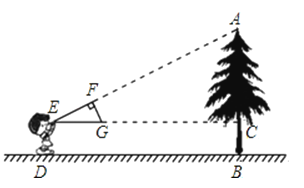
A.5m
B.5.5m
C.5.6m
D.5.8m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,CD⊥AB于D.
(1)图中有几个直角三角形;
(2)若AD=12,AC=13,则CD等于多少;
(3)若CD2=AD·DB, 求证:△ABC是直角三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将直角△ABC沿斜边AC的方向平移到△DEF的位置,,ED交BC于点G,BG=4,EF=10,△BEG的面积为4,下列结论:①∠A=∠BED;②△ABC平移的距离是4;③BE=CF;④四边形GCFE的面积为16,正确的有( )

A. ②③B. ①②③C. ①③④D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆货车从百货大楼出发负责送货,向东走了4千米到达小明家,继续向东走了1.5千米到达小红家,然后向西走了8.5千米到达小刚家,最后返回百货大楼.

(1)以百货大楼为原点,向东为正方向,1个单位长度表示1千米,请你在数轴上标出小明、小红、小刚家的位置.(小明家用点A表示,小红家用点B表示,小刚家用点C表示)
(2)小明家与小刚家相距多远?
(3)若货车每千米耗油1.5升,那么这辆货车此次送货共耗油多少升
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进![]() ,
,![]() 两种新型节能台灯共100盏,这两种台灯的进价、售价如下表:
两种新型节能台灯共100盏,这两种台灯的进价、售价如下表:
类型 | 价格 | 进价(元/盏) | 售价(元/盏) |
| 30 | 45 | |
| 50 | 70 | |
(1)若设商场购进![]() 型台灯
型台灯![]() 盏,销售完这批台灯所获利润为
盏,销售完这批台灯所获利润为![]() ,写出
,写出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)若商场规定![]() 型灯的进货数量不超过
型灯的进货数量不超过![]() 型灯数量的4倍,那么
型灯数量的4倍,那么![]() 型和
型和![]() 型台灯各进多少盏售完之后获得利润最多?此时利润是多少元.
型台灯各进多少盏售完之后获得利润最多?此时利润是多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E、F、H分别是AB、BC、CD的中点,CE、DF交于G,连接AG、HG.下列结论:①CE⊥DF;②AG=AD;③∠CHG=∠DAG;④HG=![]() AD.其中正确的有( )
AD.其中正确的有( )
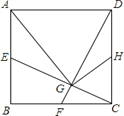
A. ① ② B. ① ② ④ C. ① ③ ④ D. ① ② ③ ④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC与△A'B'C'在平面直角坐标系中的位置如图所示
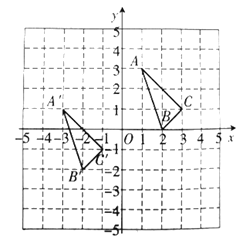
(1)分别写出下列各点的坐标:A_______ B_______ C_______
(2)△ABC由△A'B'C'经过怎样的平移得到?
(3)若点P(x,y)是△ABC内部点,则A'B'C' 内部的对应点P'的坐标为
(4)求△ABC的面积
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com