
【题目】在等边△ABC外侧作直线AP,点B关于直线AP的对称点为D,连结BD,CD,其中CD交直线AP与点E.
(1)如图1,若∠PAB=30°,则∠ACE= ;
(2)如图2,若60°<∠PAB<120°,请补全图形,判断由线段AB,CE,ED可以构成一个含有多少度角的三角形,并说明理由.

【答案】(1)30°;(2)线段AB,CE,ED可以构成一个含有60°角的三角形.
【解析】
(1)根据题意可得∠DAP=∠BAP=30°,然后根据AB=AC,∠BAC=60°,得出AD=AC,∠DAC=120°,最后根据三角形的内角和公式求解;
(2)由线段AB,CE,ED可以构成一个含有60度角的三角形,连接AD,EB,根据对称可得∠EDA=∠EBA,然后证得AD=AC,最后即可得出∠BAC=∠BEC=60°.
解:(1)连接AD,
∵点D与点B关于直线AP对称,
∴AD=AB,∠DAP=∠BAP=30°,
∵AB=AC,∠BAC=60°,
∴AD=AC,∠DAC=120°,
∴2∠ACE+120°=180°,
∴∠ACE=30°,
故答案为:30°;
(2)线段AB,CE,ED可以构成一个含有60°角的三角形.
证明:连接AD,EB,如图2.
∵点D与点B关于直线AP对称,
∴AD=AB,DE=BE,
∴∠EDA=∠EBA,
∵AB=AC,AB=AD,
∴AD=AC,
∴∠ADE=∠ACE,
∴∠ABE=∠ACE.
设AC,BE交于点F,
又∵∠AFB=∠CFE,
∴∠BAC=∠BEC=60°,
∴线段AB,CE,ED可以构成一个含有60°角的三角形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】计算题:
(1)(﹣8)+3+10+(﹣2)
(2)(﹣2)×(﹣6)÷(﹣![]() )
)
(3)(﹣1)100×2+(﹣2)3÷4
(4)2(a﹣3b)+3(2b﹣3a)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售某种商品,原价560元.随着不同幅度的降价(元),日销售量(件)发生相应变化,关系如图所示:

(1)根据图像完成下表
降价/元 | 5 | 10 | 15 | |
日销售量/件 | 780 | 840 | 870 |
(2)售价为560元时,日销售量为多少件.
(3)如果该商场要求日销售量为1110件,该商品应降价多少元.
(4)设该商品的售价为![]() 元,日销售量为
元,日销售量为![]() 件,求
件,求![]() 与
与![]() 之间的关系式.
之间的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
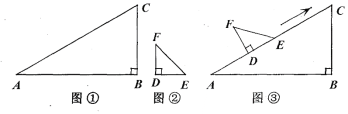
【题目】某同学在一次课外活动中,用硬纸片做了两个直角三角形,见图①、②.在图①中,∠B=90°,∠A=30°;图②中,∠D=90°,∠F=45°.图③是该同学所做的一个实验:他将△DEF的直角边DE与△ABC的斜边AC重合在一起,并将△DEF沿AC方向移动.在移动过程中,D、E两点始终在AC边上(移动开始时点D与点A重合).
(1)在△DEF沿AC方向移动的过程中,该同学发现:F、C两点间的距离逐渐 ;连接FC,∠FCE的度数逐渐 .(填“不变”、“变大”或“变小”)
(2)△DEF在移动的过程中,∠FCE与∠CFE度数之和是否为定值,请加以说明;
(3)能否将△DEF移动至某位置,使F、C的连线与AB平行?若能,求出∠CFE的度数;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了测量被池塘隔开的A,B两点之间的距离,根据实际情况,作出如图所示图形,其中AB⊥BE,EF⊥BE,AF交BE于D,C在BD上.有四位同学分别测量出以下四组数据,根据所测数据不能求出A,B间距离的是( )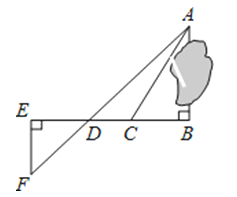
A.BC,∠ACB
B.DE,DC,BC
C.EF,DE,BD
D.CD,∠ACB,∠ADB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点D在反比例函数y= ![]() 的图象上,过点D作x轴的平行线交y轴于点B(0,3).过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC=
的图象上,过点D作x轴的平行线交y轴于点B(0,3).过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC= ![]() .
.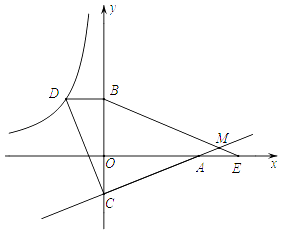
(1)求反比例函数y= ![]() 和直线y=kx+b的解析式;
和直线y=kx+b的解析式;
(2)连接CD,试判断线段AC与线段CD的关系,并说明理由;
(3)点E为x轴上点A右侧的一点,且AE=OC,连接BE交直线CA与点M,求∠BMC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,在△ABC中,AB=AC,分别以AB、BC为边作等边△ABE和等边△BCD,连结CE、AD.
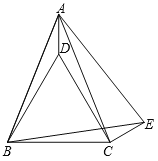
(1)求证:∠ACD=∠ABD;
(2)判断DC与CE的位置关系,并加以证明;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com