
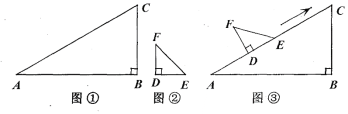
����Ŀ��ijͬѧ��һ�ο����У���ӲֽƬ��������ֱ�������Σ���ͼ�١��ڣ���ͼ���У���B=90������A=30����ͼ���У���D=90������F=45����ͼ���Ǹ�ͬѧ������һ��ʵ�飺������DEF��ֱ�DZ�DE����ABC��б��AC�غ���һ�𣬲�����DEF��AC�����ƶ������ƶ������У�D��E����ʼ����AC����(�ƶ���ʼʱ��D���A�غ�)��
(1)����DEF��AC�����ƶ��Ĺ����У���ͬѧ���֣�F��C�����ľ����� ������FC����FCE�Ķ����� �����������������������������С����
(2)��DEF���ƶ��Ĺ����У���FCE���CFE����֮���Ƿ�Ϊ��ֵ�������˵����
(3)�ܷ���DEF�ƶ���ijλ�ã�ʹF��C��������ABƽ�У����ܣ������CFE�Ķ����������ܣ���˵�����ɣ�
���𰸡���1����С�����2����ֵ����FCE+��CFE=��FED=45������3���ܣ���CFE=15����
��������
���⣨1������ͼ�εı仯�ó�F��C�����ľ���仯�ͣ���FCE�Ķ����仯���ɣ�
��2������ǵ����ʵó���FEC+��CFE=��FED=45�������ɵó��𰸣�
��3��ҪʹFC��AB��������FCE=��A=30���������ó���CFE�Ķ�����
�����������1��F��C�����ľ�����С������FC����FCE�Ķ�����ʴ�Ϊ����С�����
��2����FCE����CFE����֮��Ϊ��ֵ���������£�
�ߡ�D=90������DFE=45�������ߡ�D+��DFE+��FED=180�������FED=45�����ߡ�FED����FEC����ǣ����FEC+��CFE=��FED=45��������FCE����CFE����֮��Ϊ��ֵ��
��3��ҪʹFC��AB��������FCE=��A=30�������ߡ�CFE+��FCE=45�������CFE=45�㩁30��=15����


 ����ѧ��Ӯ�����ϵ�д�
����ѧ��Ӯ�����ϵ�д� ѧ���쳵�����ּ��������ҵ�½����������ϵ�д�
ѧ���쳵�����ּ��������ҵ�½����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ת��������ѧ�е�һ����Ҫ˼�룬����İ��������ת������Ϥ�����⣬�Ѹ��ӵ�����ת���ɼ����⣬�ѳ��������ת��Ϊ��������⣮
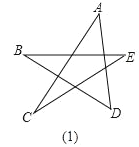
��1����������Ѿ�ѧ����֪ʶ�����������ͼ��1���С�A+��B+��C+��D+��E�Ķ�����
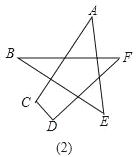
��2������ͼ��1�������ν�ȥһ���ǣ���ͼ��2�������������A+��B+��C+��D+��E+��F�Ķ�����
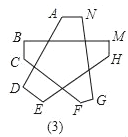
��3�����ٶ�ͼ��2���еĽǽ�һ����ȥ���������⣨2�������õķ�������ɣ�����ͼ3�еġ�A+��B+��C+��D+��E+��F+��G+��H+��M+��N�Ķ�����ֻҪд�����ۣ�����Ҫд��������̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������������ÿ̨���۷ֱ�Ϊ200Ԫ��170Ԫ��A��B�����ͺŵĵ�����������ǽ����ܵ����������
����ʱ�� | �������� | �������� | |
A���ͺ� | B���ͺ� | ||
��һ�� | 3̨ | 5̨ | 1800Ԫ |
�ڶ��� | 4̨ | 10̨ | 3100Ԫ |
(���ۡ��ۼ۾����ֲ����������������룭�����ɱ�)
(1)��A��B�����ͺŵĵ���ȵ����۵��ۣ�
(2)���������ò�����5400Ԫ�Ľ���ٲɹ��������ͺŵĵ���ȹ�30̨����A���ͺŵĵ��������ܲɹ�����̨��
(3)��(2)����������������������30̨������ܷ�ʵ������Ϊ1400Ԫ��Ŀ�ꣿ�������������Ӧ�IJɹ�����������������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������龳�����ֱ�������ķ�ͼ�����Ƶؿ̻�?��ȷ��˳���ǣ� ��
��һ��Խ��Խ����ˮ(ˮ����ʱ��Ĺ�ϵ)����һ��ȽȽ���������(�߶���ʱ��Ĺ�ϵ)������������Ա��ſ���ȥ����(�߶���ʱ��Ĺ�ϵ)����������ʻ������(�ٶ���ʱ��Ĺ�ϵ).
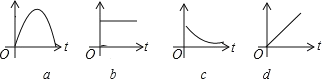
A. cdabB. acbdC. dabcD. cbad
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
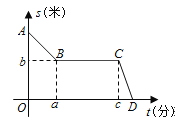
����Ŀ������ʦΪ��������һֱ��ֲ������°ࡣ��֪ѧУ������ʦ����·��Ϊ2000�ף�һ�죬����ʦ�°����45��/�ֵ��ٶȴ�ѧУ�����ߣ��ߵ���ѧУ900��ʱ����������һ�����ѣ�ͣ��������20���ӣ�֮����110��/�ֵ��ٶ����˼ң�����ʦ�ؼҹ����У���ҵ�·��S���ף�������ʱ��t���֣�֮��Ĺ�ϵ��ͼ��ʾ��
��1����a��ֵ��
��2��b= ��c= .
��3��������ʦ��ѧУ���ҵ�ƽ���ٶȡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڵȱߡ�ABC�����ֱ��AP����B����ֱ��AP�ĶԳƵ�ΪD������BD��CD������CD��ֱ��AP���E��
��1����ͼ1������PAB��30�㣬���ACE���� ����
��2����ͼ2����60�㣼��PAB��120�㣬�벹ȫͼ�Σ��ж����߶�AB��CE��ED���Թ���һ�����ж��ٶȽǵ������Σ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���з��̽�Ӧ���⣺
���г���A�ؿ���B�أ�ÿСʱ��ʻ60ǧ�ף����г�ͬʱ��B�ؿ���A�أ�ÿСʱ��ʻ90ǧ�ף���֪A��B�������200km��
��1�������ʱ������������
��2�����������ĵط���A�ض�Զ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij�˵�����ȥ̽������A����½����������4 km����������1.5 km�������ϰ�����������2 km�����ۻ����ߵ�4.5 km������һ�գ�����0.5 km���ҵ����أ��ʵ�½��A�뱦����ص�B֮��ľ����Ƕ��٣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�DE��BC����ADE=��EFC��AD��BD=5��3��CF=6����DE�ij�Ϊ�� �� 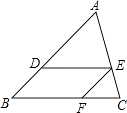
A.6
B.8
C.10
D.12
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com