
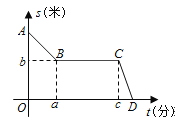
【题目】周老师为锻炼身体一直坚持步行上下班。已知学校到周老师家总路程为2000米,一天,周老师下班后,以45米/分的速度从学校往家走,走到离学校900米时,正好遇到一个朋友,停下又聊了20分钟,之后以110米/分的速度走回了家.周老师回家过程中,离家的路程S(米)与所用时间t(分)之间的关系如图所示.
(1)求a的值;
(2)b= ,c= .
(3)求周老师从学校到家的平均速度。
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:
X | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
下列结论:
①ac<0;
②当x>1时,y的值随x值的增大而减小.
③3是方程ax2+(b﹣1)x+c=0的一个根;
④当﹣1<x<3时,ax2+(b﹣1)x+c>0.
其中正确的个数为( )
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 “低碳生活,绿色出行”是我们倡导的一种生活方式,有关部门抽样调查了某单位员工上下班的交通方式,绘制了如下统计图:

(1)填空:样本中的总人数为 ;开私家车的人数m= ;扇形统计图中“骑自行车”所在扇形的圆心角为 度;
(2)补全条形统计图;
(3)该单位共有2000人,积极践行这种生活方式,越来越多的人上下班由开私家车改为骑自行车.若步行,坐公交车上下班的人数保持不变,问原来开私家车的人中至少有多少人改为骑自行车,才能使骑自行车的人数不低于开私家车的人数?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,点D在边BC上,∠ABC:∠ACB:∠ADB=1:2:3,⊙O是△ABD的外接圆.
(1)求证:AC是⊙O的切线;
(2)当BD是⊙O的直径时(如图2),求∠CAD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一个饮料包装盒剪开,铺平,纸样如图所示,包装盒的高为15cm,底面周长为40cm,包装盒底面的长为xcm.
(1)用x表示包装盒底面的宽;
(2)用x表示包装盒的表面积和体积;
(3)若包装盒底面的长为12cm,求包装盒的表面积、体积.


查看答案和解析>>
科目:初中数学 来源: 题型:
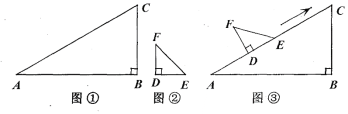
【题目】某同学在一次课外活动中,用硬纸片做了两个直角三角形,见图①、②.在图①中,∠B=90°,∠A=30°;图②中,∠D=90°,∠F=45°.图③是该同学所做的一个实验:他将△DEF的直角边DE与△ABC的斜边AC重合在一起,并将△DEF沿AC方向移动.在移动过程中,D、E两点始终在AC边上(移动开始时点D与点A重合).
(1)在△DEF沿AC方向移动的过程中,该同学发现:F、C两点间的距离逐渐 ;连接FC,∠FCE的度数逐渐 .(填“不变”、“变大”或“变小”)
(2)△DEF在移动的过程中,∠FCE与∠CFE度数之和是否为定值,请加以说明;
(3)能否将△DEF移动至某位置,使F、C的连线与AB平行?若能,求出∠CFE的度数;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
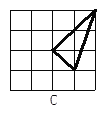
【题目】如图在4个均由16个小正方形组成的网格正方形中,各有一个格点三角形,那么这4个正方形中,与众不同的是_________,不同之处:______________.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明同学用自制的直角三角形纸板EFG测量树的高度AB,他调整自己的位置,设法使斜边EG保持水平,并且边EF所在的直线经过点A.已知纸板的两条直角边EF=60cm,FG=30cm,测得小刚与树的水平距离BD=8m,边EG离地面的高度DE=1.6m,则树的高度AB等于( )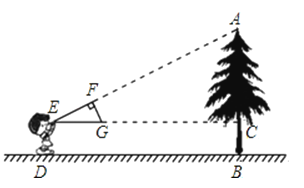
A.5m
B.5.5m
C.5.6m
D.5.8m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进![]() ,
,![]() 两种新型节能台灯共100盏,这两种台灯的进价、售价如下表:
两种新型节能台灯共100盏,这两种台灯的进价、售价如下表:
类型 | 价格 | 进价(元/盏) | 售价(元/盏) |
| 30 | 45 | |
| 50 | 70 | |
(1)若设商场购进![]() 型台灯
型台灯![]() 盏,销售完这批台灯所获利润为
盏,销售完这批台灯所获利润为![]() ,写出
,写出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)若商场规定![]() 型灯的进货数量不超过
型灯的进货数量不超过![]() 型灯数量的4倍,那么
型灯数量的4倍,那么![]() 型和
型和![]() 型台灯各进多少盏售完之后获得利润最多?此时利润是多少元.
型台灯各进多少盏售完之后获得利润最多?此时利润是多少元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com