
����Ŀ����һ����·��˳����A��B��C���أ��ס�������ͬʱ��A�س������ֱ�����ǰ��B�أ�C�أ��׳�����B��ͣ��һ��ʱ���ԭ��ԭ·���أ��ҳ�����C�غ�����ԭ��ԭ·���أ��ҳ��ȼ׳���1Сʱ����A�أ��ס�������������ʻ��·��y��ǧ�ף���ʱ��x��ʱ��������������ʱ��ʼ��ʱ��֮���ͼ����ͼ��ʾ��
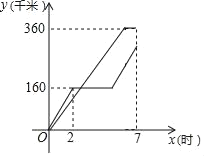
��1���������仯�����У��Ա������� ������������� ����
��2���ҳ���ʻ���ٶ�Ϊ�� ��ǧ��/Сʱ��
��3���׳�����B��ͣ���˶�ã�B����C��֮��ľ���Ϊ����ǧ�ף�
���𰸡���1��x��y����2��60����3���׳�����B��ͣ����3Сʱ��B����C��֮��ľ���Ϊ20ǧ�ף�
��������
��1�����ݺ��������Ϻ���ͼ��õ��Ա�����x���������y��
��2��������֪����֪�ҳ��ȼ׳���1Сʱ����ʻ6Сʱ�������·�̳���ʱ�伴�ɵõ��ٶȣ�
��3������ʱ��7Сʱ��ȥ����2Сʱ�õ��׳�ͣ����ʱ�䣬���ҳ���A��ʻ��C�صõ�A��C֮���·�̣��ټ�ȥ�׳���ʻ��A��B֮���·�̼��ɵõ�B��C֮���·��.
�⣺��1����ͼ��ɵã�
�Ա�����x���������y��
�ʴ�Ϊ��x��y��
��2���ҳ���ʻ���ٶ�Ϊ��360����7��1����60ǧ��/Сʱ��
�ʴ�Ϊ��60��
��3���׳�����B��ͣ���ˣ�7����2+2����3��Сʱ����
B����C��֮��ľ���Ϊ��360��2��160��20��ǧ�ף���
�𣺼׳�����B��ͣ����3Сʱ��B����C��֮��ľ���Ϊ20ǧ�ף�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��D�ڷ���������y= ![]() ��ͼ���ϣ�����D��x���ƽ���߽�y���ڵ�B��0��3��������A��5��0����ֱ��y=kx+b��y���ڵ�C����BD=OC��tan��OAC=
��ͼ���ϣ�����D��x���ƽ���߽�y���ڵ�B��0��3��������A��5��0����ֱ��y=kx+b��y���ڵ�C����BD=OC��tan��OAC= ![]() ��
��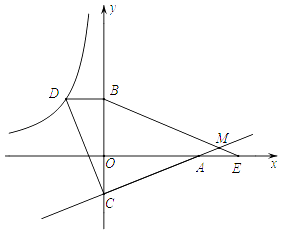
��1����������y= ![]() ��ֱ��y=kx+b�Ľ���ʽ��
��ֱ��y=kx+b�Ľ���ʽ��
��2������CD�����ж��߶�AC���߶�CD�Ĺ�ϵ����˵�����ɣ�
��3����EΪx���ϵ�A�Ҳ��һ�㣬��AE=OC������BE��ֱ��CA���M�����BMC�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������ABC�У�AB��AC���ֱ���AB��BCΪ�����ȱ���ABE�͵ȱ���BCD������CE��AD��
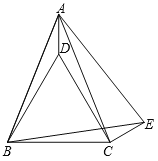
��1����֤����ACD����ABD��
��2���ж�DC��CE��λ�ù�ϵ��������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�Ǿ��Σ���E���߶�CB���ӳ����ϣ�����DE��AB�ڵ�F����AED=2��CED����G��DF���е㣬��BE=2��DF=8����AB�ij�Ϊ______ ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB��CD��CBƽ�֡�ACD����ACD��140������CBF��20������EFB��130�������CEF�Ķ�����
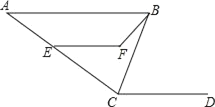
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�PM��QN�ֱ���AB��AC�Ĵ�ֱƽ���ߣ���BAC��100����ô��PAQ����(����)

A. 50�� B. 40�� C. 30�� D. 20��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ֽ��ÿ��С�����εı߳���Ϊ1���ı���ABCD���ĸ����㶼��С�����εĶ��㣨С�����εĶ���и�㣩�ϣ�����BD��

��1�����ø����ͼ�л�����ABD��AD���ϵĸߣ�����ΪH��
��2���ٻ�������ABD������ƽ��2��������ƽ��2��õ�����A1B1D1��
��ƽ�ƺ����߶�ABɨ���IJ�������ɵķ��ͼ�ε������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���P��1��0������P��1����������1����λ����P1��1��1���������ŵ�2����������2����λ����P2����1��1������3����������1����λ����P3����4����������3����λ����P4����5������������1����λ����P5����6����������4����λ����P6���������մ˹��ɣ���P��100����������P100�������ǣ� ��

A. ����26��50�� B. ����25��50�� C. ��26��50�� D. ��25��50��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬�ı���OABC�dz����Σ���A��C��D������ֱ�ΪA(9��0)��C(0��4)��D(5��0)����P�ӵ�O��������ÿ��1����λ���ȵ��ٶ���O��C��B��A�˶�����P���˶�ʱ��Ϊt�룮��t��____��ʱ����ODP������Ϊ5�ĵ��������Σ�
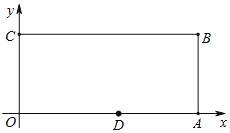
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com