
分析 在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.(1)与(2)均由勾股定理先求出另一边,在根据三角函数求角.(3)与(4)由两锐角互余求出第三个角,之后再根据三角函数求其他两边.
解答 解:(1)在Rt△ABC中,∠C=90°,a=31,c=31$\sqrt{2}$,
则:b=$\sqrt{{c}^{2}-{a}^{2}}$=$\sqrt{3{1}^{2}×2-3{1}^{2}}$=31
∵在Rt△ABC中,∠C=90°,a=b,
∴∠A=∠B=45°
(2)在Rt△ABC中,∠C=90°,a=9,b=3$\sqrt{3}$,
则:c=$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{{9}^{2}+(3\sqrt{3})^{2}}$=6$\sqrt{3}$
∵tanA=$\frac{a}{b}$=$\frac{9}{3\sqrt{3}}$=$\sqrt{3}$
∴∠A=60°,
∴∠B=90°-60°=30°
(3)在Rt△ABC中,∠C=90°,c=8$\sqrt{3}$,∠A=60°,
则:∠B=90°-60°=30°
∵直角三角形中30°的角所对边是斜边的一半,
∴b=$\frac{1}{2}$c=$\frac{1}{2}$×8$\sqrt{3}$=4$\sqrt{3}$
∴a=$\sqrt{{c}^{2}-{b}^{2}}$=$\sqrt{(8\sqrt{3})^{2}-(4\sqrt{3})^{2}}$=12
(4)在Rt△ABC中,∠C=90°,b=7.234,∠A=7°20′
则:∠B=90°-7°20′=82°40′
∵tan7°20′=$\frac{a}{b}$=$\frac{a}{7.234}$
∴a≈0.1287×7.234=0.931
又∵cosA=$\frac{b}{c}$
∴c=$\frac{b}{cosA}$≈$\frac{7.234}{cos7°20′}$=7.294
点评 本题考查了解直角三角形的问题,解题的关键是掌握解直角三角形的概念及方法.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
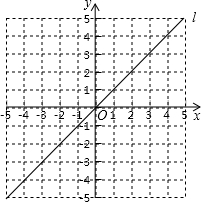 如图,在直角坐标系中,已知直线l是第一、三象限的角平分线,点A(2,0),B(3,1).
如图,在直角坐标系中,已知直线l是第一、三象限的角平分线,点A(2,0),B(3,1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
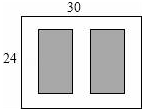 如图,某小区有一块长为30m,宽为24m的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为480m2,两块绿地之间及周边有宽度相等的人行通道,则人行通道的宽度为多少米?
如图,某小区有一块长为30m,宽为24m的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为480m2,两块绿地之间及周边有宽度相等的人行通道,则人行通道的宽度为多少米?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $-\frac{3}{2}$ | B. | $-\frac{2}{3}$ | C. | $\frac{3}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com