
分析 勾股数的定义:满足a2+b2=c2的三个正整数,称为勾股数,根据定义即可求解.
解答 解:①0.6,0.8,不是正整数,不符合勾股数的定义;
②52+122=169=132,符合勾股数的定义;
③82+152=172,符合勾股数的定义;
④42+52=41≠62,不符合勾股数的定义;
所以,可以构成勾股数有②③.
故答案为:2.
点评 本题考查了勾股数的定义,注意:
①作为勾股数的三个数必须是正整数,例如:2.5、6、6.5满足a2+b2=c2,但是它们不是正整数,所以它们不是够勾股数.
②一组勾股数扩大相同的整数倍得到三个数仍是一组勾股数.
③记住常用的勾股数再做题可以提高速度.如:3,4,5;6,8,10;5,12,13;….


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案科目:初中数学 来源: 题型:解答题
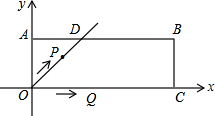 在平面直角坐标系xOy中,过原点O及点A(0,2)、C(6,0)作矩形OABC,∠AOC的平分线交AB于点D.点P从点O出发,以每秒$\sqrt{2}$个单位长度的速度沿射线OD方向移动;同时点Q从点O出发,以每秒2个单位长度的速度沿x轴正方向移动.设移动时间为t秒.
在平面直角坐标系xOy中,过原点O及点A(0,2)、C(6,0)作矩形OABC,∠AOC的平分线交AB于点D.点P从点O出发,以每秒$\sqrt{2}$个单位长度的速度沿射线OD方向移动;同时点Q从点O出发,以每秒2个单位长度的速度沿x轴正方向移动.设移动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
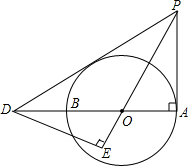 如图,AB是⊙O的直径,PA与⊙O相切于点A,PD交AB的延长线于点D,DE⊥PO交PO的延长线于点E,∠EPD=∠EDO
如图,AB是⊙O的直径,PA与⊙O相切于点A,PD交AB的延长线于点D,DE⊥PO交PO的延长线于点E,∠EPD=∠EDO查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com