解:(1)∵∠ACB=90°,PE⊥AC,PF⊥BC,
∴四边形CEPF是矩形.
∴CE=PF.
∴CE:BF=PF:BF=tanB=AC:BC=

.
(2)连DE,
∵∠ACB=90°,PE⊥CA,PF⊥BC,
∴四边形CEPF是矩形.
∴CE=PF.
∴

=

=tanB.
∵∠ACB=90°,CD⊥AB,
∴∠B+∠A=90°,∠ECD+∠A=90°,
∴∠ECD=∠B,
∴△CED∽△BFD.
∴∠EDC=∠FDB.
∵∠FDB+∠CDF=90°,
∴∠CDE+∠CDF=90°.
∴∠EDF=90°.

∵
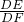
=tanB=

,
设DE=a,DF=3a,
在直角三角形EDF中,根据勾股定理可得:EF=

a.
∴

.
(3)

.
分析:(1)根据∠ACB=90°,PE⊥AC,PF⊥BC,那么CEPF就是个矩形.得到CE=PF从而不难求得CE:BF的值;
(2)可通过构建相似三角形来求解;
(3)可根据(2)的思路进行反向求解,即先通过EF,DF的比例关系,求出DE:DF的值.也就求出了CE:BF的值即tanB=AC:BC的值.
点评:本题主要考查了相似三角形的判定和性质,通过相似三角形将所求线段之间的比例关系同已知的线段间的比例关系联系在一起是解题的关键.

 如图,在△ABC中,∠ACB=90°,BC=nAC,CD⊥AB于D,点P为AB边上一动点,PE⊥AC,PF⊥BC,垂足分别为E、F.
如图,在△ABC中,∠ACB=90°,BC=nAC,CD⊥AB于D,点P为AB边上一动点,PE⊥AC,PF⊥BC,垂足分别为E、F.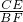 =______;
=______; 的值;
的值; =
= (直接写出结果,不需证明).
(直接写出结果,不需证明). .
. =
= =tanB.
=tanB.
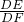 =tanB=
=tanB= ,
, a.
a. .
. .
.

 中考解读考点精练系列答案
中考解读考点精练系列答案 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为