如图所示，把一张矩形纸片对折，折痕为AB，再把以AB的中点O为顶点的平角∠AOB三等分，沿平角的三等分线折叠，将折叠后的图形剪出一个以O为顶点的等腰三角形，那么剪出的等腰三角形全部展开平铺后得到的平面图形一定是
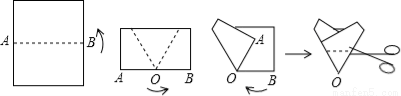
A．正三角形 B．正方形 C．正五边形 D．正六边形
科目：初中数学 来源：2014-2015学年山东省九年级中考适应性测试四数学试卷（解析版） 题型：选择题
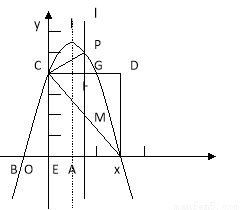
已知关于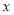
的方程
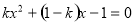，下列说法正确的是
A．当
时，方程无解
B．当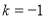
时，方程有两个相等的实数解
C．当
时，方程有一个实数解
D．当
时，方程总有两个不相等的实数解
查看答案和解析>>
科目：初中数学 来源：2014-2015学年山东省九年级学业考试预测三数学试卷（解析版） 题型：选择题
若四边形的对角线互相垂直且相等，则它一定是
A．菱形 B．正方形
C．等腰梯形 D．以上说法均不正确
查看答案和解析>>
科目：初中数学 来源：2014-2015学年山东省武城县九年级学业水平第一次模拟考试数学试卷（解析版） 题型：解答题
如图，抛物线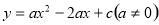
交x轴于A.B两点，A点坐标为（3,0），与y轴交于C（0,4），以OC.OA为边作矩形OADC交抛物线于点G．
（1）求抛物线的解析式；
（2）平行于抛物线对称轴的直线l在边OA（不包括O、A两点）上平行移动，分别交x轴于点E，交CD于点F，交AC于点M，交抛物线于点P，若点M的横坐标为m，请用含m的代数式表示PM的长，并求PM长的最大值。
（3）在（2）的条件下，连接PC,则在CD上方的抛物线部分是否存在这样的点P，使得以P、C.F为顶点的三角形和△AEM相似？若存在，求出此时m的值，并直接判断△PCM的形状；若不存在，请说明理由。
查看答案和解析>>
科目：初中数学 来源：2014-2015学年山东省武城县九年级学业水平第一次模拟考试数学试卷（解析版） 题型：填空题
如图4，点P在半径为3的⊙O内，OP=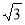
，点A为⊙O上一动点，弦AB过点P，则AB最长为_____，AB最短为______。
查看答案和解析>>
科目：初中数学 来源：2014-2015学年山东省九年级中考第三次模拟数学试卷（解析版） 题型：解答题
【课本节选】
反比例函数y= （k为常数,k≠0）的图象是双曲线.当k＞0时，双曲线两个分支分别在三象限,在每一个象限内,y随x的增大而减小（简称增减性）；反比例函数的图象关于原点对称（简称对称性）．这些我们熟悉的性质，可以通过说理得到吗？
【尝试说理】
我们首先对反比例函数y=（k＞0）的增减性来进行说理．如图，当x＞0时．
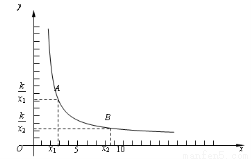
在函数图象上任意取两点A、B，设A（x1，），B（x2，），
且0＜x1＜ x2．
下面只需要比较和的大小．
—= ．
∵0＜x1＜ x2，∴x1－x2＜0，x1 x2＞0，且 k＞0．
∴＜0．即＜ ．
这说明：x1＜ x2时，＞．也就是：自变量值增大了，对应的函数值反而变小了．
即：当x＞0时，y随x的增大而减小．
同理，当x＜0时，y随x的增大而减小．
（1）试说明：反比例函数y= （k＞0）的图象关于原点对称．
【运用推广】
（2）分别写出二次函数y=ax2 （a＞0，a为常数）的对称性和增减性，并进行说理．
对称性： ；
增减性： ．
说理：
（3）对于二次函数y=ax2＋bx＋c （a＞0，a，b，c为常数），请你从增减性的角度，简要解释为何当x=— 时函数取得最小值．
查看答案和解析>>
科目：初中数学 来源：2014-2015学年山东省九年级学业水平5月模拟考数学试卷（解析版） 题型：填空题
PM2．5是指大气中直径小于或等于2．5微米的颗粒物，2．5微米等于0．000 0025米，把0．000 0025用科学记数法表示为__________．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，
，
中，最小的数是 ( )
B．0 C．
D．
的图象经过点P（
，
）和Q（
，
），则
的值为________．