
 如图,已知抛物线y=-x2+2x+c经过点C(0,3),且与x轴交于A、B两点(点A在点B的左侧),线段BC与抛物线的对称轴相交于点P.M、N分别是线段OC和x轴上的动点,运动时保持∠MPN=90°不变.
如图,已知抛物线y=-x2+2x+c经过点C(0,3),且与x轴交于A、B两点(点A在点B的左侧),线段BC与抛物线的对称轴相交于点P.M、N分别是线段OC和x轴上的动点,运动时保持∠MPN=90°不变.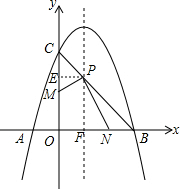 解:(1)把点C(0,3)代入y=-x2+2x+c得:
解:(1)把点C(0,3)代入y=-x2+2x+c得:
|
|
| PE |
| PF |
| PM |
| PN |
| PM |
| PN |
| 1 |
| 2 |
| 12+(2-m)2 |
| m2-4m+5 |
| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
 今年植树节,安庆某中学组织师生开展植树造林活动,为了了解全校1200名学生的植树情况,随机抽样调查50名学生的植树情况,制成如下统计表和条形统计图(均不完整).
今年植树节,安庆某中学组织师生开展植树造林活动,为了了解全校1200名学生的植树情况,随机抽样调查50名学生的植树情况,制成如下统计表和条形统计图(均不完整).| 植树数量(棵) | 频数(人) | 频率 |
| 3 | 5 | 0.1 |
| 4 | 20 | 0.4 |
| 5 | ||
| 6 | 10 | 0.2 |
| 合计 | 50 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:
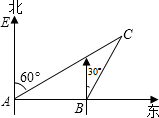 某船以每小时36海里的速度向正东方向航行,在点A测得某岛C在北偏东60°方向上,航行半小时后到达点B,测得该岛在北偏东30°方向上,已知该岛周围16海里内有暗礁.
某船以每小时36海里的速度向正东方向航行,在点A测得某岛C在北偏东60°方向上,航行半小时后到达点B,测得该岛在北偏东30°方向上,已知该岛周围16海里内有暗礁.查看答案和解析>>
科目:初中数学 来源: 题型:
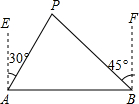 如图,城市A的正东方向100km处有一卫星城B,现计划在这两座城市间修筑一条城际快速通道(即线段AB),经测量,核能开发中心P在A城的北偏东30°和B城市的北偏西45°的方向上,已知核辐射区域是以P点为圆心50km为半径的圆形区域,请问这条快速通道会不会穿越核辐射区?请说明理由.
如图,城市A的正东方向100km处有一卫星城B,现计划在这两座城市间修筑一条城际快速通道(即线段AB),经测量,核能开发中心P在A城的北偏东30°和B城市的北偏西45°的方向上,已知核辐射区域是以P点为圆心50km为半径的圆形区域,请问这条快速通道会不会穿越核辐射区?请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
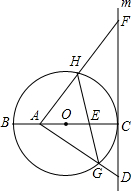 如图,⊙O的直径BC=8,过点C作⊙O的切线m,D是直线m上一点,且DC=4,A是线段BO上一动点,连结AD交⊙O于点G,过点A作AF⊥AD交直线m于点F,交⊙O于点H,连结GH交BC于点E.
如图,⊙O的直径BC=8,过点C作⊙O的切线m,D是直线m上一点,且DC=4,A是线段BO上一动点,连结AD交⊙O于点G,过点A作AF⊥AD交直线m于点F,交⊙O于点H,连结GH交BC于点E.查看答案和解析>>
科目:初中数学 来源: 题型:
 有两部不同型号的手机(分别记为A,B)和与之匹配的2个保护盖(分别记为a,b)(如图所示)散乱地放在桌子上.
有两部不同型号的手机(分别记为A,B)和与之匹配的2个保护盖(分别记为a,b)(如图所示)散乱地放在桌子上.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com