练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

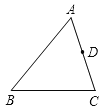
    【题目】如图，在三角形ABC中，AB＝24，AC＝18，D是AC上一点，AD=12，在AB上取一点E，使A、D、E三点组成的三角形与ABC相似，则AE＝__________.

    【答案】9或16

    【解析】试题分析：根据相似三角形的判断，要使得△ADE与△ABC相似，已经满足∠BAC＝∠DAE，因此只要两边对应成比例即可，由于本题中三角形相似，对应点没有确定，因此分两种情况，画出图形，然后根据相似三角形对应边成比例，就出AE的长.

    第一种情况：当△ABC∽△ADE时，如图①；

    ∵△ABC∽△ADE，

    ∴，

    ∵AB＝24，AC＝18，AD＝12，

    ∴，

    ∴AE＝9.

    第二种情况：当△ABC∽△AED，如图②；

    ∵△ABC∽△AED，

    ∴，

    ∵AB＝24，AC＝18，AD＝12，

    ∴，

    ∴AE＝16.

    故填9或16.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图所示，可以自由转动的转盘被3等分，指针落在每个扇形内的机会均等．

    （1）现随机转动转盘一次，停止后，指针指向1的概率为　 　；

    （2）小明和小华利用这个转盘做游戏，若采用下列游戏规则，你认为对双方公平吗？请用列表或画树状图的方法说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在东营市中小学标准化建设工程中，某学校计划购进一批电脑和电子白板，经过市场考察得知，购买1台电脑和2台电子白板需要3.5万元，购买2台电脑和1台电子白板需要2.5万元.

    （1）求每台电脑、每台电子白板各多少万元?

    （2）根据学校实际，需购进电脑和电子白板共30台，总费用不超过30万元，但不低于28万元，请你通过计算求出有几种购买方案，哪种方案费用最低.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为增强环保意识，某社区计划开展一次“减碳环保，减少用车时间”的宣传活动，对部分家庭五月份的平均每天用车时间进行了一次抽样调查，并根据收集的数据绘制了下面两幅不完整的统计图．请根据图中提供的信息，解答下列问题：

    （1）本次抽样调查了多少个家庭？

    （2）将图①中的条形图补充完整，直接写出用车时间的中位数落在哪个时间段内；

    （3）求用车时间在1～1.5小时的部分对应的扇形圆心角的度数；

    （4）若该社区有车家庭有1600个，请你估计该社区用车时间不超过1.5小时的约有多少个家庭？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

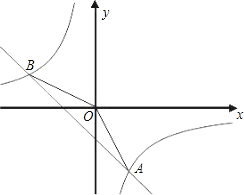
    【题目】已知一次函数y= kx+b的图象与反比例函数的图象相交于A，B两点， 其中A点的横坐标与B点的纵坐标都是2，如图：

    （1）求这个一次函数的解析式；

    （2）在y轴是否存在一点P使△OAP为等腰三角形？若存在，请求出符合条件的点P坐标；若不存在，请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知，△ABC是等边三角形，四边形ACFE是平行四边形，AE＝BC．

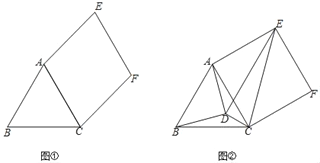
    (1)如图①，求证：ACFE是菱形；

    (2)如图②，点D是△ABC内一点，且∠ADB＝90°，∠EDC＝90°，∠ABD＝∠ACE．求证：ACFE是正方形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC 和△BDE 都是等边三角形，A、B、D 三点共线.下列结论：①AB＝CD；②BF＝BG；③HB 平分∠AHD；④∠AHC＝60°，⑤△BFG 是等边三角形．其中正确的有____________（只填序号）.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，已知正方形ABCD的边长为1，点E在边BC上，若∠AEF=90°，且EF交正方形的外角∠DCM的平分线CF于点F．

    （1）图1中若点E是边BC的中点，我们可以构造两个三角形全等来证明AE=EF，请叙述你的一个构造方案，并指出是哪两个三角形全等（不要求证明）；

    （2）如图2，若点E在线段BC上滑动（不与点B，C重合）．

    ①AE=EF是否一定成立？说出你的理由；

    ②在如图2所示的直角坐标系中抛物线y=ax2+x+c经过A、D两点，当点E滑动到某处时，点F恰好落在此抛物线上，求此时点F的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在菱形ABCD中，∠BAD＝120°，CE⊥AD，且CE＝BC，连接BE交对角线AC于点F，则∠EFC＝_____°．

    查看答案和解析>>

    同步练习册答案