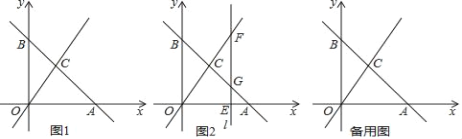
如图1，平面直角坐标系中，直线y=kx+b与x轴交于点A（6，0），与y轴交于点B，与直线y=2x交于点C（a，4）．
（1）求点C的坐标及直线AB的表达式；
（2）如图2，在（1）的条件下，过点E作直线l⊥x轴于点E，交直线y=2x于点F，交直线y=kx+b于点G，若点E的坐标是（4，0）．
①求△CGF的面积；
②直线l上是否存在点P，使OP+BP的值最小？若存在，直接写出点P的坐标；若不存在，说明理由；
（3）若（2）中的点E是x轴上的一个动点，点E的横坐标为m（m＞0），当点E在x轴上运动时，探究下列问题：
当m取何值时，直线l上存在点Q，使得以A，C，Q为顶点的三角形与△AOC全等？请直接写出相应的m的值．
世纪百通期末金卷系列答案科目：初中数学 来源：河北省张家口市宣化县2018届九年级中考数学模拟试卷（四） 题型：单选题
如图，为了测量河对岸l1上两棵古树A、B之间的距离，某数学兴趣小组在河这边沿着与AB平行的直线l2上取C、D两点，测得∠ACB=15°，∠ACD=45°，若l1、l2之间的距离为50m，则A、B之间的距离为（ ）
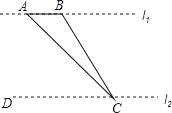
A. 50m B. 25m C. （50﹣
）m D. （50﹣25
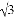）m
查看答案和解析>>
科目：初中数学 来源：北京师大实验中学2018年中考数学模拟试卷 题型：填空题
《九章算术》是中国传统数学最重要的著作，在“勾股”章中有这样一个问题：“今有邑方二百步，各中开门，出东门十五步有木，问：出南门几步而见木？”
用今天的话说，大意是：如图，
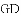
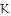
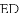
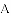
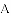
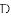
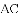
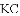
查看答案和解析>>
科目：初中数学 来源：天津市第四联合学区2019届九年级上学期第二次月考数学试卷 题型：单选题
如图，在边长为1的正方形构成的网络中，半径为1的⊙O的圆心在格点上，则图中阴影部分两个小扇形的面积之和为（ ）
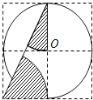
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中数学 来源：天津市第四联合学区2019届九年级上学期第二次月考数学试卷 题型：单选题
如图，△ABC内接于⊙O，AB=BC，∠ABC=120°，AD为⊙O的直径，AD＝10， 那么BD＝（ ）
A. 8 B. 5 C. 8
D. 5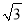
查看答案和解析>>
科目：初中数学 来源：山东省青岛市、五十九中2018-2019学年八年级（上）联考期中数学试卷 题型：解答题
已知一次函数y=kx+b的图象经过点A（1，2），B（0，4）．
（1）求此函数的解析式．
（2）求原点到直线AB的距离．
查看答案和解析>>
科目：初中数学 来源：山东省青岛市、五十九中2018-2019学年八年级（上）联考期中数学试卷 题型：填空题
定义：如图，点P、Q把线段AB分割成线段AP、PQ和BQ，若以AP、PQ、BQ为边的三角形是一个直角三角形，则称点P、Q是线段AB的勾股分割点．已知点P、Q是线段AB的勾股分割点，如果AP＝4，PQ＝6(PQ＞BQ)，那么BQ＝________ .
查看答案和解析>>
科目：初中数学 来源：沪科版九年级数学上册_第23章_解直角三角形_单元同步测试卷 题型：解答题
峨眉河是峨眉的一个风景点．如图，河的两岸
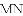
，然后沿河岸走了
，求这条河的宽度（参考数据：
，
）．
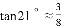查看答案和解析>>
科目：初中数学 来源：广东省2018-2019学年八年级上学期期中考试数学试卷 题型：单选题
甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500m，先到终点
的人原地休息．已知甲先出发2s．在跑步过程中，甲、乙两人的距离y(m)与乙出发的时间t(s)之间的关系
如图所示，给出以下结论：①a＝8；②b＝92；③c＝123．其中正确的是【 】
A．①②③ B．仅有①② C．仅有①③ D．仅有②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
