
 的两个实数根.
的两个实数根. 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:不详 题型:解答题
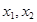 分别是一元二次方程
分别是一元二次方程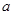
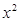 +
+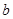
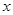 +
+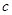 =0(
=0(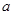 ≠0)的两根,请你解决下列问题:
≠0)的两根,请你解决下列问题: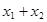 =-
=-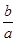 ,
,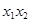 =
=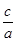
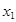 ,
,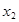 是方程
是方程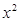 -4
-4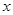 +2=0的两个实根,利用根与系数的关系求
+2=0的两个实根,利用根与系数的关系求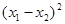 的值;
的值;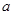 ,cos
,cos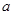 (
(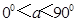 )是关于x的方程2
)是关于x的方程2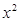 -
-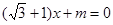 的两个根,求角
的两个根,求角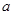 的度数.
的度数.查看答案和解析>>
科目:初中数学 来源:不详 题型:计算题
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 没有实数根,即不存在一个实数的平方等于
没有实数根,即不存在一个实数的平方等于 .若我们规定一个新数“
.若我们规定一个新数“ ”,使其满足
”,使其满足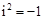 (即方程
(即方程 有一个根为
有一个根为 ).并且进一步规定:一切实数可以与新数进行四则运算,且原有运算律和运算法则仍然成立,于是有
).并且进一步规定:一切实数可以与新数进行四则运算,且原有运算律和运算法则仍然成立,于是有 ,从而对于任意正整数
,从而对于任意正整数 ,我们可以得到
,我们可以得到 ,同理可得
,同理可得 ,
, ,
, .那么
.那么 的值为 .
的值为 .查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.289(1―2x)=256 | B.256(1+x)2=289 |
| C.289(1―x)2=256 | D.289―289(1―x)―289(1―x)2=256 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com