
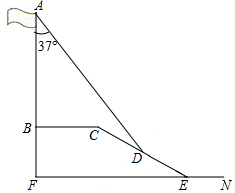
 在学习解直角三角形以后,重庆八中数学兴趣小组测量了旗杆的高度.如图,某一时刻,旗杆AB的影子一部分落在平台上的影长BC为6米,落在斜坡上的影长CD为4米,AB⊥BC,同一时刻,光线与旗杆的夹角为37°,斜坡的坡角为30°,旗杆的高度AB约为( )米.(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,$\sqrt{3}$≈1.73)
在学习解直角三角形以后,重庆八中数学兴趣小组测量了旗杆的高度.如图,某一时刻,旗杆AB的影子一部分落在平台上的影长BC为6米,落在斜坡上的影长CD为4米,AB⊥BC,同一时刻,光线与旗杆的夹角为37°,斜坡的坡角为30°,旗杆的高度AB约为( )米.(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,$\sqrt{3}$≈1.73)| A. | 10.61 | B. | 10.52 | C. | 9.87 | D. | 9.37 |
分析 作CG⊥EF、延长GH交AD于点H、作HP⊥AB可得四边形BCHP为矩形,从而知BC=PH=6、BP=CH、∠CHD=∠A=37°,先求出AP$\frac{PH}{tan∠A}$=8,作DQ⊥GH知∠CDQ=∠CEG=30°,求出CQ=2、DQ=2$\sqrt{3}$,再求得QH=$\frac{DQ}{tan∠CHD}$=$\frac{8\sqrt{3}}{3}$\CH=QH-CQ=$\frac{8\sqrt{3}}{3}$-2,根据AB=AP+PB=AP+CH可得答案.
解答 解:如图,过点C作CG⊥EF于点G,延长GH交AD于点H,过点H作HP⊥AB于点P,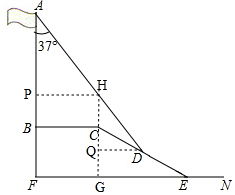
则四边形BCHP为矩形,
∴BC=PH=6,BP=CH,∠CHD=∠A=37°,
∴AP=$\frac{PH}{tan∠A}$=$\frac{6}{0.75}$=8,
过点D作DQ⊥GH于点Q,
∴∠CDQ=∠CEG=30°,
∴CQ=$\frac{1}{2}$CD=2,DQ=CDcos∠CDQ=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,
∵QH=$\frac{DQ}{tan∠CHD}$=$\frac{2\sqrt{3}}{0.75}$=$\frac{8\sqrt{3}}{3}$,
∴CH=QH-CQ=$\frac{8\sqrt{3}}{3}$-2,
则AB=AP+PB=AP+CH=8+$\frac{8\sqrt{3}}{3}$-2≈10.61,
故选:A.
点评 本题主要考查解直角三角形、三角函数,坡脚等知识,解题的关键是正确添加辅助线,构造直角三角形解决问题.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:填空题
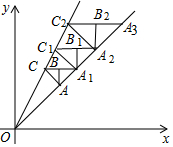 如图,在平面直角坐标系第一象限内,直线y=x与直线y=2x的内部作等腰Rt△ABC,是∠ABC=90°,边BC∥x轴,AB∥y轴,点A(1,1)在直线y=x上,点C在直线y=2x上:CB的延长线交直线y=x于点A1,作等腰Rt△A1B1C1,是∠A1B1C1=90°,B1C1∥x轴,A1B1∥y轴,点C1在直线y=2x上…按此规律,则等腰Rt△AnBnCn的腰长为$\frac{{4}^{n}}{{3}^{n+1}}$.
如图,在平面直角坐标系第一象限内,直线y=x与直线y=2x的内部作等腰Rt△ABC,是∠ABC=90°,边BC∥x轴,AB∥y轴,点A(1,1)在直线y=x上,点C在直线y=2x上:CB的延长线交直线y=x于点A1,作等腰Rt△A1B1C1,是∠A1B1C1=90°,B1C1∥x轴,A1B1∥y轴,点C1在直线y=2x上…按此规律,则等腰Rt△AnBnCn的腰长为$\frac{{4}^{n}}{{3}^{n+1}}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明和爸爸进行登山锻炼,两人同时从山脚下出发,沿相同路线匀速上山,小明用8分钟登上山顶,此时爸爸距出发地280米.小明登上山顶立即沿原路按某一速度匀速下山,与爸爸相遇后,和爸爸一起以原下山速度返回出发地.小明、爸爸在锻炼过程中离出发地的路程y1(米)、y2(米)与小明出发的时间x(分)的函数关系如图.
小明和爸爸进行登山锻炼,两人同时从山脚下出发,沿相同路线匀速上山,小明用8分钟登上山顶,此时爸爸距出发地280米.小明登上山顶立即沿原路按某一速度匀速下山,与爸爸相遇后,和爸爸一起以原下山速度返回出发地.小明、爸爸在锻炼过程中离出发地的路程y1(米)、y2(米)与小明出发的时间x(分)的函数关系如图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=-x2+bx+c与直线AB交于A(-4,-4),B(0,4)两点,直线AC:y=-$\frac{1}{2}$x-6交y轴于点C.点E是直线AB上的动点,过点E作EF⊥x轴交AC于点F,交抛物线于点G.
如图,抛物线y=-x2+bx+c与直线AB交于A(-4,-4),B(0,4)两点,直线AC:y=-$\frac{1}{2}$x-6交y轴于点C.点E是直线AB上的动点,过点E作EF⊥x轴交AC于点F,交抛物线于点G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
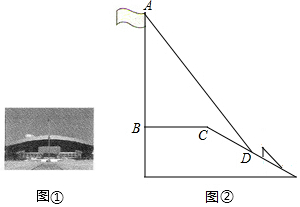 深圳市民中心广场上有旗杆如图①所示,某学校兴趣小组测量了该旗杆的高度,如图②,某一时刻,旗杆AB的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长BC为16米,落在斜坡上的影长CD为8米,AB⊥BC;同一时刻,太阳光线与水平面的夹角为45°.1米的标杆EF竖立在斜坡上的影长FG为2米,求旗杆的高度.
深圳市民中心广场上有旗杆如图①所示,某学校兴趣小组测量了该旗杆的高度,如图②,某一时刻,旗杆AB的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长BC为16米,落在斜坡上的影长CD为8米,AB⊥BC;同一时刻,太阳光线与水平面的夹角为45°.1米的标杆EF竖立在斜坡上的影长FG为2米,求旗杆的高度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 12 | B. | 15 | C. | 14 | D. | 20 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com