练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    [探究创新]

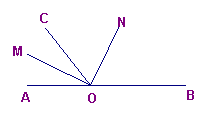
    如图，O是直线AB上的一点，OM是∠AOC的角平分线，ON是∠BOC的角平分线，

    （1）图中互余的角有几对？

    （2）图中互补的角有几对？

      (1)  4   (2) 5

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    （创新学习）如图，等腰三角形与正三角形的形状有差异，我们把等腰三角形与正三角形的接近程度称为“正度”．在研究“正度”时，应保证相似三角形的“正度”相等．
    精英家教网
    设等腰三角形的底和腰分别为a，b，底角和顶角分别为α，β．要求“正度”的值是非负数．
    同学甲认为：可用式子|a-b|来表示“正度”，|a-b|的值越小，表示等腰三角形越接近正三角形；
    同学乙认为：可用式子|α-β|来表示“正度”，|α-β|的值越小，表示等腰三角形越接近正三角形．
    探究：（1）他们的方案哪个较合理，为什么？
    （2）对你认为不够合理的方案，请加以改进（给出式子即可）；
    （3）请再给出一种衡量“正度”的表达式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （拓展创新）在教材中，我们通过数格子的方法发现了直角三角形的三边关系，利用完全相同的四个直角三角形采用拼图的方式验证了勾股定理的正确性．
    精英家教网
    问题1：以直角三角形的三边为边向形外作等边三角形，探究S1+S2与S3的关系（如图1）．
    问题2：以直角三角形的三边为斜边向形外作等腰直角三角形，探究S′+S″与S的关系（如图2）．
    问题3：以直角三角形的三边为直径向形外作半圆，探究S1+S2与S3的关系（如图3）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    40、（创新探究题）如图所示，已知E，F分别是矩形ABCD的边BC，CD上两点，连接AE，BF，请你再从下面四个反映图中边角关系的式子：①AB=BC；②BE=CF；③AE=BF；④∠AEB=∠BFC中选出两个作为已知条件，一个作为结论，组成一个命题，并证明这个命题是否正确（只需写出一种情况）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

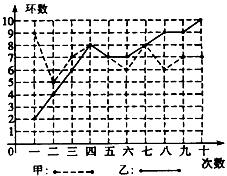    精英家教网（创新探究题）甲，乙两人在相同条件下各射靶10次，每次射靶的成绩情况如图所示，请从下列四个不同的角度对这次测试结果进行分析：
    （1）从平均数和方差相结合看，优胜者是
     
    ；
    （2）从平均数和中位数相结合看，优胜者是
     
    ；
    （3）从平均数和命中9环以上的次数相结合看，优胜者是
     
    ；
    （4）从折线图上两人射击命中环数的走势看，潜力更大的是
     
    ．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    （创新探究题）如图所示，已知E，F分别是矩形ABCD的边BC，CD上两点，连接AE，BF，请你再从下面四个反映图中边角关系的式子：①AB=BC；②BE=CF；③AE=BF；④∠AEB=∠BFC中选出两个作为已知条件，一个作为结论，组成一个命题，并证明这个命题是否正确（只需写出一种情况）．
    精英家教网

    查看答案和解析>>

    同步练习册答案