
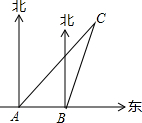
 如图所示,某船向正东方向航行,在A处望见某岛C在北偏东45°方向,前进6海里到达B处,测得该岛在北偏东30°方向,已知在该岛周围6海里内有暗礁,若该船继续向东航行,有无触礁的危险?请说明理由.
如图所示,某船向正东方向航行,在A处望见某岛C在北偏东45°方向,前进6海里到达B处,测得该岛在北偏东30°方向,已知在该岛周围6海里内有暗礁,若该船继续向东航行,有无触礁的危险?请说明理由. 分析 判断有无危险只要求出点C到AB的距离,与6海里比较大小就可以.
解答 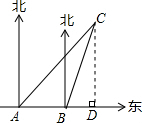 解:若该船继续向东航行,无触礁的危险.理由如下:
解:若该船继续向东航行,无触礁的危险.理由如下:
过点C作CD⊥AB于点D,
由题意得:∠CAD=45°,∠CBD=90°-30°=60°,
在Rt△CBD中,∵tan∠CBD=$\frac{CD}{BD}$,
∴BD=$\frac{CD}{tan∠CBD}$=$\frac{\sqrt{3}}{3}$CD.
在等腰Rt△CBD中,CD=AD.
又∵AD-BD=6,
∴CD-$\frac{\sqrt{3}}{3}$CD=6,
解得CD=9+3$\sqrt{3}$>6,
即:若船继续向东航行,无触礁危险.
点评 本题是将实际问题转化为直角三角形中的数学问题,可通过作辅助线构造直角三角形,再把条件和问题转化到这个直角三角形中,使问题解决.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:选择题
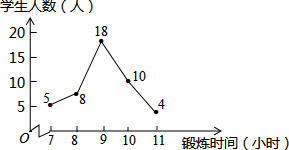 某班体育委员统计了全班45名同学一周的体育锻炼时间,并绘制了如图所示的折线统计图,则在体育锻炼时间这组数据中,众数和中位数分别是( )
某班体育委员统计了全班45名同学一周的体育锻炼时间,并绘制了如图所示的折线统计图,则在体育锻炼时间这组数据中,众数和中位数分别是( )| A. | 18,18 | B. | 9,9 | C. | 9,10 | D. | 18,9 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{10}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{5}{8}$ | C. | $\frac{45}{64}$ | D. | $\frac{49}{64}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com