
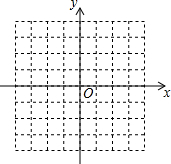

分析 (1)首先把不等式x+2>-x+4移项、合并同类项,再化简可得2x-2>0,然后画一次函数y=2x-2的图象,再根据图象可直接得到答案;
(2)画出一次函数y=2x+2,y=-x+5的图象,根据图象可得答案.
解答 解:(1)x+2>-x+4可变形为2x-2>0,
画一次函数y=2x-2的图象,如图所示:
根据图象可得:当x>1时,图象在x轴的上方,
故不等式x+2>-x+4的解集为:x>1;
(2)画出一次函数y=2x+2,y=-x+5,
由图象可知,当-1<x<1时,y=2x+2的图象在x轴上方且在直线y=-x+5,
故不等式组0<2x+2<-x+5的解集为:-1<x<1.
点评 此题主要考查了一次函数与一元一次不等式,关键是正确作出函数图象,从函数的角度看,就是寻求使一次函数y=ax+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作⊙O的切线,交AB于点E,交CA的延长线于点F.
如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作⊙O的切线,交AB于点E,交CA的延长线于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
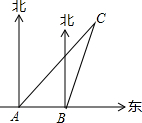 如图所示,某船向正东方向航行,在A处望见某岛C在北偏东45°方向,前进6海里到达B处,测得该岛在北偏东30°方向,已知在该岛周围6海里内有暗礁,若该船继续向东航行,有无触礁的危险?请说明理由.
如图所示,某船向正东方向航行,在A处望见某岛C在北偏东45°方向,前进6海里到达B处,测得该岛在北偏东30°方向,已知在该岛周围6海里内有暗礁,若该船继续向东航行,有无触礁的危险?请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
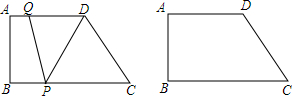
 如图,AC∥CD,AP和CP分别平分∠BAC和∠ACD,过点P分别作PG⊥AC于点G,PE⊥AB于点E,EP的延长线交CD于点F.
如图,AC∥CD,AP和CP分别平分∠BAC和∠ACD,过点P分别作PG⊥AC于点G,PE⊥AB于点E,EP的延长线交CD于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com