
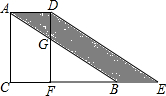
 将直角三角形ABC沿CB方向平移CF的长度后,得到直角三角形DEF.已知DG=4,CF=6,AC=10,求阴影部分的面积.
将直角三角形ABC沿CB方向平移CF的长度后,得到直角三角形DEF.已知DG=4,CF=6,AC=10,求阴影部分的面积.  小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:选择题
 的概率是( )
的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{5}{8}$ | C. | $\frac{3}{5}$ | D. | $\frac{3}{8}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{5}{8}$ | C. | $\frac{45}{64}$ | D. | $\frac{49}{64}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
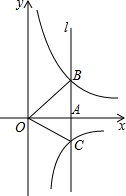 如图,经过点A(3,0)的直线l平行于y轴,与双曲线y=$\frac{4}{x}$和y=$\frac{k}{x}$分别交于点B和C.
如图,经过点A(3,0)的直线l平行于y轴,与双曲线y=$\frac{4}{x}$和y=$\frac{k}{x}$分别交于点B和C.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
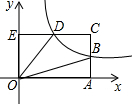 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象交矩形OECA的边AC于B点,交CE于D点,且B是AC的中点,若四边形ODCB的面积是5,则k=5.
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象交矩形OECA的边AC于B点,交CE于D点,且B是AC的中点,若四边形ODCB的面积是5,则k=5.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com