
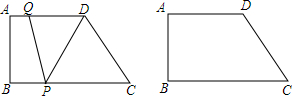
分析 (1)分点P未到达点C时和点P在BC延长线上两种情况,用t表示出QD、CP,然后根据平行四边形对边相等列出方程求解即可;
(2)①PD=PQ时,过P作PE⊥AD于E,根据等腰三角形三线合一的性质用t表示出QE,然后表示出AE,再根据AE=AP列出方程求解;
②DQ=PQ,过Q作QF⊥BC于F,用t表示出FP,在Rt△QPF中,利用勾股定理列出方程求解即可.
解答  解:(1)①如图1,P未到达C点时,
解:(1)①如图1,P未到达C点时,
∵四边形PCDQ是平行四边形,
∴16-t=21-2t,
解得t=5;
②点P在BC延长线上时,
∵四边形CPDQ是平行四边形,
∴16-t=2t-21,
解得t=$\frac{37}{3}$,
综上所述,以P、Q、C、D为顶点的四边形是平行四边形,t的值是5或$\frac{37}{3}$;
(2)①如图2,若PD=PQ,过P作PE⊥AD于E,
则QD=16-t,QE=$\frac{1}{2}$QD=$\frac{1}{2}$(16-t),
AE=AQ+QE=t+$\frac{1}{2}$(16-t)=$\frac{1}{2}$(16+t),
∵AE=BP,
∴$\frac{1}{2}$(16+t)=2t,
解得t=$\frac{16}{3}$;
②如图3,若DQ=PQ,过Q作QF⊥BC于F,
则QF=8,FP=2t-t=t,
在Rt△QPF中,由勾股定理得:
QF2+FP2=QP2,
即82+t2=(16-t)2,
解得t=6.
点评 本题考查了梯形的性质,平行四边形的对边相等的性质,等腰三角形的判定与性质,勾股定理的应用,综合题,但难度不大,作辅助线利用等腰三角形三线合一的性质以及勾股定理是解题的关键.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:解答题
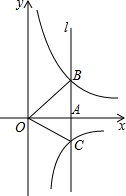 如图,经过点A(3,0)的直线l平行于y轴,与双曲线y=$\frac{4}{x}$和y=$\frac{k}{x}$分别交于点B和C.
如图,经过点A(3,0)的直线l平行于y轴,与双曲线y=$\frac{4}{x}$和y=$\frac{k}{x}$分别交于点B和C.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
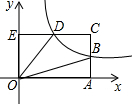 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象交矩形OECA的边AC于B点,交CE于D点,且B是AC的中点,若四边形ODCB的面积是5,则k=5.
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象交矩形OECA的边AC于B点,交CE于D点,且B是AC的中点,若四边形ODCB的面积是5,则k=5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
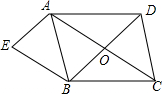 如图,在?ABCD中,对角线AC、BD相交于点O,AE∥BD,BE∥AC,AE与BE相交于点E,当AB,AD满足什么条件时,四边形AEBO为矩形?请说明埋由.
如图,在?ABCD中,对角线AC、BD相交于点O,AE∥BD,BE∥AC,AE与BE相交于点E,当AB,AD满足什么条件时,四边形AEBO为矩形?请说明埋由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com