
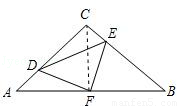
��ͼ���ڵ���Rt��ABC�У���C=90�㣬AC=8��F��AB���ϵ��е㣬��D��E�ֱ���AC��BC�����˶����ұ���AD=CE������DE��DF��EF���ڴ��˶��仯�Ĺ����У����н��ۣ�
�١�DFE�ǵ���ֱ�������Σ����ı���CDFE������Ϊ�����Σ���DE���ȵ���СֵΪ4�����ı���CDFE��������ֲ��䣻�ݡ�CDE��������ֵΪ8��
������ȷ�Ľ����ǣ� ��

A���٢ڢ� B���٢ۢ� C���٢ܢ� D���ۢܢ�
C.
��������
�������������CF���ߡ�ABC�ǵ���ֱ�������Σ����FCB=��A=45�㣬CF=AF=FB����AD=CE�����ADF�ա�CEF����EF=DF����CFE=��AFD���ߡ�AFD+��CFD=90�㣬���CFE+��CFD=��EFD=90�㣬���EDF�ǵ���ֱ�������Σ���ˢ���ȷ��
��D��E�ֱ�ΪAC��BC�е�ʱ���ı���CDFE�������Σ��ˢڴ���
���ڡ�DEF�ǵ���ֱ�������Σ���˵�DE��Сʱ��DFҲ��С������DF��ACʱ��DE��С����ʱDF=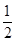 AC=4����DE=
AC=4����DE=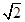 DF=
DF=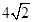 ����ˢ۴���
����ˢ۴���
�ߡ�ADF�ա�CEF����S��CEF=S��ADF��S�ı���CEFD=S��AFC����ˢ���ȷ��
����CEF������ʱ���ɢ�֪����ʱ��DEF�������С����ʱS��CDE=S�ı���CEFD��S��DEF=S��AFC��S��DEF=16��8=8����ˢ���ȷ����ѡC��
���㣺1������ֱ�������Σ�2��ȫ�������ε��ж������ʣ�


 ���ٴ�����ɽ����ϵ�д�
���ٴ�����ɽ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ���ڵ���Rt��ABC�У���C=90�㣬AC=8��F��AB���ϵ��е㣬��D��E�ֱ���AC��BC�����˶����ұ���AD=CE������DE��DF��EF���ڴ��˶��仯�Ĺ����У����н��ۣ�
��ͼ���ڵ���Rt��ABC�У���C=90�㣬AC=8��F��AB���ϵ��е㣬��D��E�ֱ���AC��BC�����˶����ұ���AD=CE������DE��DF��EF���ڴ��˶��仯�Ĺ����У����н��ۣ�| A���٢ڢ� | B���٢ܢ� | C���٢ۢ� | D���ۢܢ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ���˶����ұ���AD=CE������DE��DF��EF��
���˶����ұ���AD=CE������DE��DF��EF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ���ڵ���Rt��ABC�У���ACB=90�㣬CA=CB����M��N��AB���������㣬�ҡ�MCN=45�㣬��TΪAB���е㣮���½��ۣ���AB=
��ͼ���ڵ���Rt��ABC�У���ACB=90�㣬CA=CB����M��N��AB���������㣬�ҡ�MCN=45�㣬��TΪAB���е㣮���½��ۣ���AB=| 2 |
| A���٢ڢۢ� | B��ֻ�Т٢ڢ� |
| C��ֻ�Т٢ۢ� | D��ֻ�Тڢ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ���ڵ���Rt��ABC�У���C=90�㣬AC=8
��ͼ���ڵ���Rt��ABC�У���C=90�㣬AC=8| 2 |
| 2 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com