
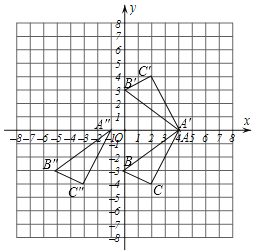
【题目】已知△ABC的三个顶点A,B,C的坐标分别为A(4,0),B(0,-3),C(2,-4).

(1)在如图的平面直角坐标系中画出△ABC关于x轴对称的△A'B'C',并分别写出A′,B′,C′的坐标;
(2)将△ABC向左平移5个单位,请画出平移后的△A″B″C″,并写出△A″B″C″各个顶点的坐标;
(3)求出(2)中的△ABC在平移过程中所扫过的面积.
【答案】(1)A′(4,0),B′(0,3),C′(2,4);(2)A″(-1,0),B″(-5,-3),C″(-3,-4);(3)25
【解析】试题分析:(1)根据网格结构找出点A、B、C以及点A′,B′,C′位置,然后顺次连接即可,再根据平面直角坐标系写出各点的坐标;
(2)根据网格结构找出点A、B、C向左平移5个单位的对应点A″、B″、C″,然后顺次连接即可,再根据平面直角坐标系写出各点的坐标;
(3)根据△ABC扫过的面积等于一个平行四边形的面积加上△ABC的面积列式计算即可得解.
试题解析:解:(1)△ABC如图所示,A′(4,0),B′(0,3),C′(2,4);
(2)△A″B″C″如图所示,A″(﹣1,0),B″(﹣5,﹣3),C″(﹣3,﹣4);
(3)△ABC在平移过程中所扫过的面积=5×4+(4×4﹣![]() ×4×3﹣
×4×3﹣![]() ×1×2﹣
×1×2﹣![]() ×2×4)=20+(16﹣6﹣1﹣4)=20+5=25.
×2×4)=20+(16﹣6﹣1﹣4)=20+5=25.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】如图ΔABC中,∠B =∠C,BD=CF,BE=CD,∠EDF=α,则下列结论正确的是( )

A. 2α+∠A=90° B. 2α+∠A=180°
C. α+∠A=90° D. α+∠A=180°
查看答案和解析>>
科目:初中数学 来源: 题型:
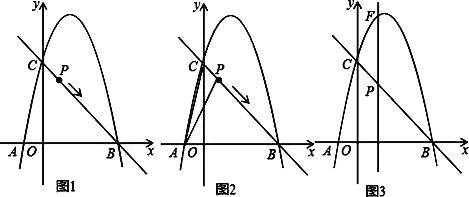
【题目】如图1,抛物线y=ax2+bx+5的图象过A(﹣1,0),B(5,0)两点,与y轴交于点C,作直线BC,动点P从点C出发,以每秒![]() 个单位长度的速度沿CB向点B运动,运动时间为t秒,当点P与点B重合时停止运动.
个单位长度的速度沿CB向点B运动,运动时间为t秒,当点P与点B重合时停止运动.
(1)求抛物线的表达式;
(2)如图2,当t=1时,若点Q是X轴上的一个动点,如果以Q,P,B为顶点的三角形与△ABC相似,求出Q点的坐标;
(3)如图3,过点P向x轴作垂线分别交x轴,抛物线于E、F两点.
①求PF的长度关于t的函数表达式,并求出PF的长度的最大值;
②连接BF,将△PBF沿BF折叠得到△P′BF,当t为何值时,四边形PFP′B是菱形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=![]() ,AF=
,AF=![]() ,求AE的长.
,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
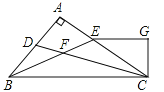
【题目】如图,△ABC的角平分线 CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:①∠CEG=2∠DCB;②CA平分∠BCG;③∠ADC=∠GCD;④∠DFB=![]() ∠CGE.
∠CGE.
其中正确的结论是_____________(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx+b的图像经过点(-1.-5),且与正比例函数y=![]() x的图象相交于点(2,m).
x的图象相交于点(2,m).
(1)求m的值;
(2)求一次函数y=kx+b的解析式;
(3)求这两个函数图像与x轴所围成的三角形面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】保护生态环境,建设绿色社会已经从理念变为人们的行动.某化工厂2009年1 月的利润为200万元.设2009年1 月为第1个月,第x个月的利润为y万元.由于排污超标,该厂决定从2009年1 月底起适当限产,并投入资金进行治污改造,导致月利润明显下降,从1月到5月,y与x成反比例.到5月底,治污改造工程顺利完工,从这时起,该厂每月的利润比前一个月增加20万元(如图).

⑴分别求该化工厂治污期间及治污改造工程完工后y与x之间对应的函数关系式.
⑵治污改造工程完工后经过几个月,该厂月利润才能达到2009年1月的水平?
⑶当月利润少于100万元时为该厂资金紧张期,问该厂资金紧张期共有几个月?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)、如图(1),AB∥CD,点P在AB、CD外部,若∠B=40°,∠D=15°,则∠BPD °.
(2)、如图(2),AB∥CD,点P在AB、CD内部,则∠B,∠BPD,∠D之间有何数量关系?证明你的结论;
(3)、在图(2)中,将直线AB绕点B按逆时针方向旋转一定角度交直线CD于点M,如图(3),若∠BPD=90°,∠BMD=40°,求∠B+∠D的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=BC=AC=12cm,现有两点M、N分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为1cm/s,点N的速度为2cm/s.当点N第一次到达B点时,M、N同时停止运动.

(1)点M、N运动几秒后,M、N两点重合?
(2)点M、N运动几秒后,可得到等边三角形△AMN?
(3)当点M、N在BC边上运动时,能否得到以MN为底边的等腰三角形?如存在,请求出此时M、N运动的时间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com