
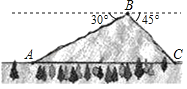
【题目】我市304国道通辽至霍林郭勒段在修建过程中经过一座山峰,如图所示,其中山脚A、C两地海拔高度约为1000米,山顶B处的海拔高度约为1400米,由B处望山脚A处的俯角为30°,由B处望山脚C处的俯角为45°,若在A、C两地间打通一隧道,求隧道最短为多少米(结果取整数,参考数据![]() ≈1.732)
≈1.732)
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
【题目】某校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食,为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图.
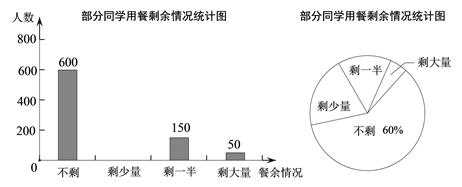
(1)这次被调查的同学共有 人;
(2)补全条形统计图,并在图上标明相应的数据;
(3)校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供50人食用一餐.据此估算,该校18 000名学生一餐浪费的食物可供多少人食用一餐.
查看答案和解析>>
科目:初中数学 来源: 题型:
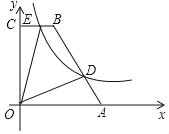
【题目】如图,在四边形OABC中,BC∥AO,∠AOC=90°,点A,B的坐标分别为(5,0),(2,6),点D为AB上一点,且![]() ,双曲线y=
,双曲线y=![]() (k>0)经过点D,交BC于点E
(k>0)经过点D,交BC于点E
(1)求双曲线的解析式;
(2)求四边形ODBE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地图书馆为了满足群众多样化阅读的需求,决定购买甲、乙两种品牌的电脑若干组建电子阅览室.经了解,甲、乙两种品牌的电脑单价分别3100元和4600元.
(1)若购买甲、乙两种品牌的电脑共50台,恰好支出200000元,求甲、乙两种品牌的电脑各购买了多少台?
(2)若购买甲、乙两种品牌的电脑共50台,每种品牌至少购买一台,且支出不超过160000元,共有几种购买方案?并说明哪种方案最省钱.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,给出五个等量关系:①AD=BC;②AC=BD;③CE=DE;④∠D=∠C;⑤∠DAB=∠CBA.
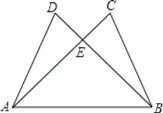
请你以其中两个为条件,另外三个中的一个为结论,推出一个正确的结论(只需写出一种情况),并加以证明.
已知:
求证:
证明:
查看答案和解析>>
科目:初中数学 来源: 题型:
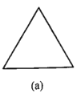
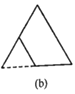
【题目】如图所示,图(a)是一块边长为1,周长记为![]() 的正三角形纸板,沿图(a)的底边剪去一块边长为
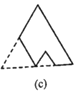
的正三角形纸板,沿图(a)的底边剪去一块边长为![]() 的正三角形纸板后得到图(b),然后沿同一底边依次剪去一块更小的正三角形纸板(即其边长为前一块被剪掉正三角形纸板边长的
的正三角形纸板后得到图(b),然后沿同一底边依次剪去一块更小的正三角形纸板(即其边长为前一块被剪掉正三角形纸板边长的![]() 后,得图(c),(d),……,记第
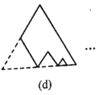
后,得图(c),(d),……,记第![]() )块纸板的周长为Pn.则
)块纸板的周长为Pn.则![]() ____;
____;![]() _______.
_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形纸片ABCD沿其对角线AC折叠,使点B落在点B′的位置,AB′与CD交于点E.
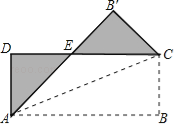
(1)求证:△AED≌△CEB′;
(2)求证:点E在线段AC的垂直平分线上;
(3)若AB=8,AD=3,求图中阴影部分的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】7张如图1的长为a,宽为b(a>b)的小长方形纸片,按图2的方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )
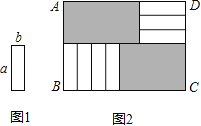
A.a=![]() bB.a=3bC.a=
bB.a=3bC.a=![]() bD.a=4b
bD.a=4b
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com