
 如图,某人由西向东行走到点A,测得一个圆形花坛的圆心O在北偏东60°,他继续向东走了60米后到达点B,这时测得圆形花坛的圆心O在北偏东45°,已知圆形花坛的半径为51米,若沿AB的方向修一条笔直的小路(忽略小路的宽度),则此小路会通过圆形花坛吗?请说明理由.(参考数据$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41)
如图,某人由西向东行走到点A,测得一个圆形花坛的圆心O在北偏东60°,他继续向东走了60米后到达点B,这时测得圆形花坛的圆心O在北偏东45°,已知圆形花坛的半径为51米,若沿AB的方向修一条笔直的小路(忽略小路的宽度),则此小路会通过圆形花坛吗?请说明理由.(参考数据$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41) 分析 过点O作OD⊥AB于D,在Rt△OBD和Rt△OAD中,根据三角函数AD,BD就可以OD表示出来,根据AB=60米,就得到一个关于OD的方程,求得OD.从而可以判断此小路是否会通过圆形花坛.
解答 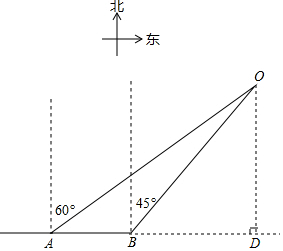 解:此小路会通过圆形花坛.
解:此小路会通过圆形花坛.
理由:过点O作OD⊥AC,交AB延长线于D.
设OD为x米,在Rt△OBD中,
∠OBD=90°-45°=45°.
∴BD=OD=x米.
在Rt△OAD中,
∵∠OAD=90°-60°=30°
∴AD=$\frac{x}{tan30°}$=$\sqrt{3}$x,
∵AD=AB+BD,
∴$\sqrt{3}$x=60+x,
∴x=$\frac{60}{\sqrt{3}-1}$=30($\sqrt{3}$+1)>51,
∴此小路会通过圆形花坛.
点评 本题主要考查解直角三角形在实际问题中的应用,构造直角三角形是解题的前提和关键.


科目:初中数学 来源: 题型:解答题
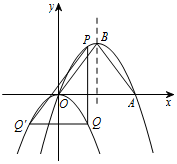 如图,抛物线y=-$\frac{4}{9}$x2+bx+c经过原点和点A(6,0),与其对称轴交于点B,P是抛物线y=-$\frac{4}{9}$x2+bx+c上一动点,且在x轴上方.过点P作x轴的垂线交动抛物线y=-$\frac{4}{9}$(x-h)2(h为常数)于点Q,过点Q作PQ的垂线交动抛物线y=-$\frac{4}{9}$(x-h)2于点Q′(不与点Q重合),连结PQ′,设点P的横坐标为m.
如图,抛物线y=-$\frac{4}{9}$x2+bx+c经过原点和点A(6,0),与其对称轴交于点B,P是抛物线y=-$\frac{4}{9}$x2+bx+c上一动点,且在x轴上方.过点P作x轴的垂线交动抛物线y=-$\frac{4}{9}$(x-h)2(h为常数)于点Q,过点Q作PQ的垂线交动抛物线y=-$\frac{4}{9}$(x-h)2于点Q′(不与点Q重合),连结PQ′,设点P的横坐标为m.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 不在同一条直线上的三个点确定一个圆 | |
| B. | 相等的圆心角所对的弧相等 | |
| C. | 平分弦的直径垂直于弦 | |
| D. | 在同圆或等圆中,相等的弦所对的圆周角相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
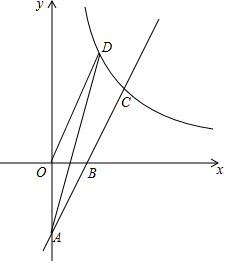 如图,在平面直角坐标系中,直线y=kx-4(k≠0)与坐标轴交于A、B两点,与反比例函数y=$\frac{m}{x}$(m≠0,x>0)在第一象限内的图象交于点C(4,a),反比例函数图象上有一点D(b,6),连接OD和AD,已知:tan∠OAB=$\frac{1}{2}$.
如图,在平面直角坐标系中,直线y=kx-4(k≠0)与坐标轴交于A、B两点,与反比例函数y=$\frac{m}{x}$(m≠0,x>0)在第一象限内的图象交于点C(4,a),反比例函数图象上有一点D(b,6),连接OD和AD,已知:tan∠OAB=$\frac{1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
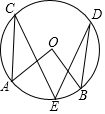 如图,点A、B、C、D、E在⊙O上,若∠ACE=25°,∠BDE=15°,则圆心角∠AOB的大小为( )
如图,点A、B、C、D、E在⊙O上,若∠ACE=25°,∠BDE=15°,则圆心角∠AOB的大小为( )| A. | 90° | B. | 85° | C. | 80° | D. | 40° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com