
 如图,在等腰三角形ABC中AB=AC,AD⊥BC点D,BE⊥AC于点E,AD与BE交于点P,BP=3,PE=1,求三角形BDP的面积.
如图,在等腰三角形ABC中AB=AC,AD⊥BC点D,BE⊥AC于点E,AD与BE交于点P,BP=3,PE=1,求三角形BDP的面积. 分析 如图,作辅助线,构建△BCE的中位线,利用三角形中位线定理易求PG、AG的长度,并得EC=2DG,设DG=x,则EC=2x,利用同角的三角函数列式可求x的值,最后由三角形面积公式进行解答.
解答 解:如图,过D作DG⊥BE于G,
∵AB=AC,AD⊥BC,
∴BD=CD,即点D是BC的中点,
∵BE⊥AC,
∴DG∥AC,
∴BG=EG,
∴GD是△BCE的中位线,
∴DG=$\frac{1}{2}$CE.即CE=2DG,
∵BP=3,PE=1,
∴BE=3+1=4,
∴BG=$\frac{1}{2}$BE=2,
∴PG=3-2=1,
设DG=x,则EC=2x,
在△APE和△BPD中,∵∠BPD=∠APE,
∠BDP=∠AEP=90°,
∴∠DAC=∠DBP=∠GDP,
tan∠DBP=tan∠GDP=$\frac{EC}{BE}$,
∴$\frac{2x}{4}=\frac{1}{x}$,
x=$±\sqrt{2}$,
∴DG=$\sqrt{2}$,
∴S△BDP=$\frac{1}{2}$GD•BP=$\frac{1}{2}$×$\sqrt{2}$×3=$\frac{3\sqrt{2}}{2}$;
故答案为:$\frac{3\sqrt{2}}{2}$
点评 本题考查了三角形中位线定理,等腰三角形三线合一的性质,三角函数,如果没学三角函数可利用证明△DGP∽△BEC列比例式得出面积.


科目:初中数学 来源: 题型:选择题
| A. | -$\sqrt{3}$ | B. | -1.5 | C. | $-\sqrt{2}$ | D. | -1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 天数 | 2 | 3 | 4 | 6 |
| 降雨量(毫米) | 8 | 6 | 7 | 5 |
| A. | 8,5 | B. | 8,7 | C. | 5,8 | D. | 5,6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为点D,E,AD与BE交于点F,BF=AC,∠ABE=22°,∠CAD的度数是( )
如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为点D,E,AD与BE交于点F,BF=AC,∠ABE=22°,∠CAD的度数是( )| A. | 23° | B. | 22° | C. | 32° | D. | 33° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
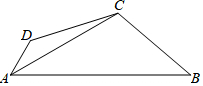 如图,已知四边形ABCD中,AC平分∠DAB,∠DAB=60°,∠B与∠D互补,AC=4,CD=3,则AB-AD=2$\sqrt{5}$.
如图,已知四边形ABCD中,AC平分∠DAB,∠DAB=60°,∠B与∠D互补,AC=4,CD=3,则AB-AD=2$\sqrt{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,点A、B的坐标分别为(1,1)、(1,2),过点A、B分别作y轴的垂线,垂足为D、C,得到正方形ABCD,抛物线y=x2+bx+c经过A、C两点,点P为第一象限内抛物线上一点(不与点A重合),过点P分别作x轴y轴的垂线,垂足为E、F,设点P的横坐标为m,矩形PFOE与正方形ABCD重叠部分图形的周长为l.
如图,在平面直角坐标系中,点A、B的坐标分别为(1,1)、(1,2),过点A、B分别作y轴的垂线,垂足为D、C,得到正方形ABCD,抛物线y=x2+bx+c经过A、C两点,点P为第一象限内抛物线上一点(不与点A重合),过点P分别作x轴y轴的垂线,垂足为E、F,设点P的横坐标为m,矩形PFOE与正方形ABCD重叠部分图形的周长为l.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某人由西向东行走到点A,测得一个圆形花坛的圆心O在北偏东60°,他继续向东走了60米后到达点B,这时测得圆形花坛的圆心O在北偏东45°,已知圆形花坛的半径为51米,若沿AB的方向修一条笔直的小路(忽略小路的宽度),则此小路会通过圆形花坛吗?请说明理由.(参考数据$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41)
如图,某人由西向东行走到点A,测得一个圆形花坛的圆心O在北偏东60°,他继续向东走了60米后到达点B,这时测得圆形花坛的圆心O在北偏东45°,已知圆形花坛的半径为51米,若沿AB的方向修一条笔直的小路(忽略小路的宽度),则此小路会通过圆形花坛吗?请说明理由.(参考数据$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com