��֪�����κ���y=x2+��n-2m��x+m2-mn��
��1����֤���˶��κ�����x���н��㣻
��2����m-1=0����֤����x2+��n-2m��x+m2-mn=0��һ��ʵ����Ϊ1��
��3���ڣ�2���������£��跽��x2+��n-2m��x+m2-mn=0����һ��Ϊa����x=2ʱ������n �ĺ���y1=nx+am��y2=x2+��n-2m��ax+m2-mn��ͼ���ڵ�A��B����A�ڵ�B����ࣩ��ƽ����y���ֱ��L��y1=nx+am��y2=x2+��n-2m��ax+m2-mn��ͼ��ֱ��ڵ�C��D����
CD=6�����C��D�����꣮
�⣺��1��֤������y=0������x2+��n-2m��x+m2-mn=0��
�ߡ�=��n-2m��2-4��m2-mn��=n2��
��n2��0��
�����0��
����κ���y=x2+��n-2m��x+m2-mn��x���н��㣻
��2���⣺�ⷨһ����m-1=0����m=1��
���x2+��n-2m��x+m2-mn=0�ɻ�Ϊx2+��n-2��x+1-n=0��
��ã�x=1��x=1-n��
���x2+��n-2m��x+m2-mn=0��һ��ʵ����Ϊ1��
�ⷨ������m-1=0��m=1��
���x2+��n-2m��x+m2-mn=0�ɻ�Ϊx2+��n-2��x+1-n=0��
��x=1ʱ���������=1+��n-2��+1-n=0�������ұ�=0��
�����=�ұߣ�
���x2+��n-2m��x+m2-mn=0��һ��ʵ����Ϊ1��
��3���⣺����x2+��n-2m��x+m2-mn=0�ĸ��ǣ�x1=1��x2=1-n��
��a=1-n��
��x=2ʱ��y1=n+1��y2=-2n2+5n+1��
���C��b��b+1����
���D��b��-2b2+5b+1����
��CD=6��
��b+1-��-2b2+5b+1��=6��-2b2+5b+1-��b+1��=6��
��b=3��b=-1��
��C��D���������ֱ�ΪC��3��4����D��3��-2����C��-1��0����D��-1��-6����
��������1��������y=0������x2+��n-2m��x+m2-mn=0���ٸ����б�ʽ�жϴ˷��̸������������֤�ô˶��κ�����x���н��㣻
��2����m-1=0���������m��ֵ����m��ֵ����ԭ������⣬�����һ��Ϊ1����m=1���뷽�̣��ɵ÷�������������ȣ����֤�÷���x2+��n-2m��x+m2-mn=0��һ��ʵ����Ϊ1��
��3���ɷ���x2+��n-2m��x+m2-mn=0�ĸ��ǣ�x1=1��x2=1-n���ɵ�a=1-n�����ɵ�x=2ʱ��y1=n+1��y2=-2n2+5n+1�����C��b��b+1��������CD=6���������b��ֵ��������ý⣮
���������⿼���˶��κ�����һԪ���η��̵Ĺ�ϵ���б�ʽ�Լ������ľ����֪ʶ�������ۺ��Խ�ǿ������Ĺؼ���ע�ⷽ��˼���Ӧ�ã�




 ��֪�����κ����ı���ʽΪy=2x2+4x-1��
��֪�����κ����ı���ʽΪy=2x2+4x-1��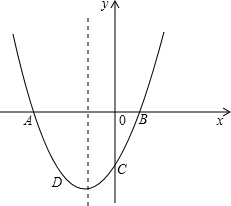 ���ڵ�C����D��-2��-3�����������ϣ�
���ڵ�C����D��-2��-3�����������ϣ�