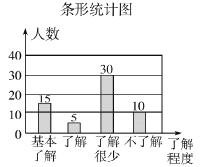
【题目】“校园安全”受到全社会的广泛关注，东营市某中学对部分学生就校园安全知识的了解程度，采用随机抽样调查的方式，并根据收集到的信息进行统计，绘制了下面两幅尚不完整的统计图．请你根据统计图中所提供的信息解答下列问题：

（1）接受问卷调查的学生共有_______人，扇形统计图中“基本了解”部分所对应扇形的圆心角为_______°；

（2）请补全条形统计图；

（3）若该中学共有学生900人，请根据上述调查结果，估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数；

（4）若从对校园安全知识达到“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛，请用树状图或列表法求出恰好抽到1个男生和1个女生的概率．

参考答案：

【答案】（1）60,90°；（2）详见解析；（3）300；（4）.

【解析】

试题分析：（1）在扇形图中找到“了解很少”所占的百分比，在条形图中找出“了解很少”所对应的人数，据此即可求出接受问卷调查的学生总人数；在条形图中找出“基本了解”部分的人数，用这个人数除以接受调查的总人数所得的商再乘以360°，即可求出扇形统计图中“基本了解”部分所对应扇形的圆心角的度数.（2）先用接受调查总人数-“基本了解”的人数-“基本了解”的人数-“不了解”的人数，算出“了解”的人数，再根据“了解”的人数补全条形统计图.（3）利用总人数900乘以“了解”和“基本了解”所对应的百分比即可求解．（4）首先根据题意列出表格，然后由表格求得所有等可能的结果以及一男一女参加比赛的情况，再利用概率公式即可求得答案．

试题解析：（1）60,90°；

（2） 补全条形统计图如图所示：

（3） 根据题意得：900×＝300（人），

则估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数为300人．

（4） 列表法如图所示：

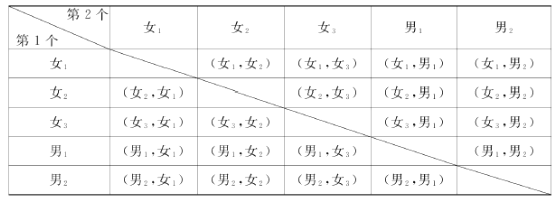
则所有等可能的情况有20种，其中选中1个男生和1个女生的情况有12种，所以恰好抽到1个男生和1个女生的概率：P＝＝.

关闭