
【题目】如图,在△ABC中,以BC为直径的圆交AC于点D,∠ABD=∠ACB.

(1)求证:AB是圆的切线;
(2)若点E是BC上一点,已知BE=4 ,tan∠AEB=![]() ,AB∶BC=2∶3,求圆的直径.
,AB∶BC=2∶3,求圆的直径.
【答案】(1)详见解析;(2)10.
【解析】
试题分析:(1)根据∠ABD=∠ACB和∠ACB+∠DBC= 90°可得∠ABC=90°,然后根据切线的判定定理可判断AB是圆的切线;(2) 根据BE=4 ,tan∠AEB=![]() 先求出AB的长,再根据AB∶BC=2∶3求出BC的长,即得直径.
先求出AB的长,再根据AB∶BC=2∶3求出BC的长,即得直径.
试题解析:(1)证明:∵BC是直径,∴∠BDC=90°,∴∠ACB+∠DBC= 90°.
又∵∠ABD=∠ACB,∴∠ABD+∠DBC=90°,∴AB⊥BC.
又∵点B在圆上,∴AB是圆的切线.
(2)解:在Rt△AEB中,tan∠AEB=![]() ,∴
,∴![]() =
=![]() ,即AB=
,即AB=![]() BE=
BE=![]() ×4=
×4=![]() .
.
∵AB∶BC=2∶3,∴BC=![]() AB=
AB=![]() ×
×![]() =10.
=10.
∴圆的直径为10.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
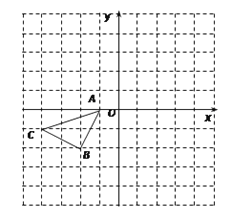
【题目】如图所示的正方形网格中,△ABC 的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:
(1)以A点为旋转中心,将△ABC绕点A顺时针旋转90°得△AB1C1,画出△AB1C1.
(2)作出△ABC关于坐标原点O成中心对称的△A2B2C2.
(3)作出点C关于x轴的对称点P. 若点P向右平移x个单位长度后落在△A2B2C2的内部(不含落在△A2B2C2的边上),请直接写出x的取值范围.
(提醒:每个小正方形边长为1个单位长度)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)沿海某市企业计划投入800万元购进A、B两种小型海水淡化设备,这两种设备每台的购入价、每台设备每天可淡化的海水量及淡化率如下表:
每台购入价(万元) | 每台每天可淡化海水量(立方米) | 淡化率 | |
A型 | 20 | 250 | 80% |
B型 | 25 | 400 | 75% |
(1)若该企业每天能生产9000立方米的淡化水,求购进A型、B型设备各几台?
(2)在(1)的条件下,已知每淡化1立方米海水所需的费用为1.5元,政府补贴0.3元.企业将淡化水以3.2元/立方米的价格出售,每年还需各项支出61万元.按每年实际生产300天计算,该企业至少几年后能收回成本(结果精确到个位)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注,东营市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:

(1)接受问卷调查的学生共有_______人,扇形统计图中“基本了解”部分所对应扇形的圆心角为_______°;
(2)请补全条形统计图;
(3)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数;
(4)若从对校园安全知识达到“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在射线BA,BC,AD,CD围成的菱形ABCD中,∠ABC=60°,AB=6![]() ,O是射线BD上一点,⊙O与BA,BC都相切,与BO的延长线交于点M.过M作EF⊥BD交线段BA(或射线AD)于点E,交线段BC(或射线CD)于点F.以EF为边作矩形EFGH,点G,H分别在围成菱形的另外两条射线上.
,O是射线BD上一点,⊙O与BA,BC都相切,与BO的延长线交于点M.过M作EF⊥BD交线段BA(或射线AD)于点E,交线段BC(或射线CD)于点F.以EF为边作矩形EFGH,点G,H分别在围成菱形的另外两条射线上.

(1)求证:BO=2OM.
(2)设EF>HE,当矩形EFGH的面积为24![]() 时,求⊙O的半径.
时,求⊙O的半径.
(3)当HE或HG与⊙O相切时,求出所有满足条件的BO的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com