B
分析:根据等腰三角形的性质和三角形内角和定理由AB=AC,∠A=36°可得到∠B=∠ACB=72°,再根据线段垂直平分线的性质得到DA=DC,根据等腰三角形的性质有∠ACD=∠A=36°,可计算出∠BCD=72°-36°=36°,∠BDC=180°-∠B-∠BCD=72°,则CB=CD,可对①进行判断;根据三角形的角平分线的定义可对②进行判断;根据DA=DC和
三角形周长的定义可得到△BCD的周长C△BCD=DB+DC+BC=DB+DA+BC=AB+BC,则可对③进行判断;由于△ADM为直角三角形,而△BCD为顶角为36°的等腰三角形,
可对④进行判断.
解答:∵AB=AC,∠A=36°,
∴∠B=∠ACB=72°,
∵AC的垂直平分线MN交AB于D,
∴DA=DC,
∴∠ACD=∠A=36°,
∴∠BCD=72°-36°=36°,
∴∠BDC=180°-∠B-∠BCD=72°,
∴CB=CD,
∴△BCD是等腰三角形,所以①正确;
∵∠BCD=36°,∠ACD=36°,
∴CD平分∠ACB,
∴线段CD为△ACB的角平分线,所以②错误;
∵DA=DC,
∴△BCD的周长C△BCD=DB+DC+BC=DB+DA+BC=AB+BC,所以③正确;
∵△ADM为直角三角形,而△BCD为顶角为36°的等腰三角形,
∴△ADM不等全等于△BCD,所以④错误.
故选C.
点评:本题考查了全等三角形的判定与性质:有两组边对应相等,且它们所夹的角也相等,那么这两个三角形全等;全等三角形的对应边相等.也考查了线段垂直平分线的性质以及等腰三角形的判定与性质.

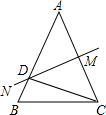 如图,已知AB=AC,∠A=36°,AC的垂直平分线MN交AB于D,AC于M.以下结论:
如图,已知AB=AC,∠A=36°,AC的垂直平分线MN交AB于D,AC于M.以下结论:

 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案