练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
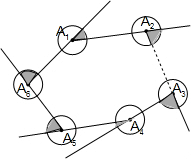
    7．如图所示，分别以n边形的顶点为圆心，以1cm为半径画园，当n=2017时则图中阴影部分的面积之和为（　　）
    A．πcm2B．2πcm2C．2016πcm2D．2017πcm2

    分析 由于多边形的外角和为360°，则所有阴影的扇形的圆心角的和为360度，故阴影部分的面积=π×12=π．

    解答 解：∵多边形的外角和为360°，
    ∴SA1+SA2+…+SA2017=S圆=π×12=π（cm2）．
    故选A．

    点评 本题考查了圆的面积公式的应用，多边形的外角和定理，比较简单．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    17．如图1，已知l1∥l2，点A，B在直线l1上，点C，D在l2上，连接AD，BC．AE，CE分别是∠BAD，∠BCD的平分线，∠1=70°，∠2=30°．
    （1）求∠AEC的度数；
    （2）如图2，将线段AD沿线段CD方向平移，其他条件不变，求∠AEC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    18．如图，平行四边形ABCD中，E、F是对角线BD上的两点，在不添加任何辅助线的情况下，如果添加一个条件使△ABE≌△CDF，则添加的条件是BE=FD或BF=DE或∠1=∠2（答案不唯一）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．关于x的不等式组$\left\{\begin{array}{l}{x＞a}\\{x＜1}\end{array}\right.$的解集为无解，则a的取值范围是（　　）
    A．a＞1B．a＜1C．a≥1D．a≤1

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共30只，某小组做摸球实验，将球搅匀后从中随机摸出一个球记下颜色，再把它放回袋中，不断重复．下表是活动进行中的一组统计数据：
    摸球的次数n1001502005008001000…
    摸到白球的次数m5896116295484601…
    摸到白球的频率0.580.640.580.590.6050.601…
    （1）请估计：当n很大时，摸到白球的频率将会接近0.60；
    （2）假如你去摸一次，你摸到白球的概率是0.60，摸到黑球的概率是0.40；
    （3）试估算口袋中黑、白两种颜色的球各有多少只？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．设函数y=-x+5与y=$\frac{3}{x}$的图象的两个交点的横坐标为a、b，则$\frac{1}{a}$+$\frac{1}{b}$的值是$\frac{5}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．如图，AB∥DE，∠B=80°，CM平分∠BCD，CN⊥CM，求∠NCE的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．下列运算正确的是（　　）
    A．$\root{3}{-1}=-\root{3}{-1}$B．$\root{3}{-3}=\root{3}{3}$C．$\root{3}{-1}=\root{3}{{|{-1}|}}$D．$\root{3}{-1}=-\root{3}{1}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．下列算式（1）3$\sqrt{2}$-4$\sqrt{2}$=-1；（2）5$\sqrt{3}$+5$\sqrt{2}$=10$\sqrt{5}$；（3）5$\sqrt{x}$•5$\sqrt{y}$=5$\sqrt{xy}$；（4）2$\sqrt{\frac{x}{y}}$÷$\sqrt{\frac{x}{9y}}$=6；（5）a$\sqrt{-\frac{1}{a}}$=-$\sqrt{-a}$．其中正确的有（　　）
    A．3个B．2个C．1个D．0个

    查看答案和解析>>

    同步练习册答案