[题目]计算:|﹣|﹣(﹣π)0﹣sin30°+(﹣)﹣2 题目和参考答案——青夏教育精英家教网—

【题目】计算：|﹣|﹣（﹣π）0﹣sin30°+（﹣）﹣2

【答案】解：原式=﹣1﹣+4
=3．
【解析】先分别根据绝对值的性质、零指数幂及负整数幂的计算法则、特殊角的三角函数值分别计算出各数的值，再根据实数混合运算的法则进行计算即可．
【考点精析】本题主要考查了零指数幂法则和整数指数幂的运算性质的相关知识点，需要掌握零次幂和负整数指数幂的意义： a0=1（a≠0）;a-p=1/ap（a≠0，p为正整数）；aman=am+n(m、n是正整数)；（am）n=amn(m、n是正整数)；(ab)n=anbn(n是正整数)；am/an=am-n(a不等于0，m、n为正整数）；（a/b）n=an/bn(n为正整数)才能正确解答此题．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】解不等式组，并在数轴上表示不等式组的解集．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】我们知道：垂直于弦的直径平分这条弦，并且平分这条弦所对的两条弧；平分弧的直径垂直平分这条弧所对的弦．你可以利用这一结论解决问题：
如图，点P在以MN（南北方向）为直径的⊙O上，MN=8，PQ⊥MN交⊙O于点Q，垂足为H，PQ≠MN，弦PC、PD分别交MN于点E、F，且PE=PF．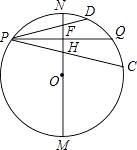

（1）比较与的大小；
（2）若OH=2 ，求证：OP∥CD；
（3）设直线MN、CD相交所成的锐角为α，试确定cosα= 时，点P的位置．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】已知函数y1=ax2+bx，y2=ax+b（ab≠0）．在同一平面直角坐标系中．
（1）若函数y1的图象过点（﹣1，0），函数y2的图象过点（1，2），求a，b的值．
（2）若函数y2的图象经过y1的顶点．
①求证：2a+b=0；
②当1＜x＜时，比较y1 ， y2的大小．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】抛物线y=ax2+bx+c的图象如图所示，则一次函数y=ax+b与反比例函数y=在同一平面直角坐标系内的图象大致为（　　）

A.
B.
C.
D.

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，AB为⊙O的直径，PD切⊙O于点C，与BA的延长线交于点D，DE⊥PO交PO延长线于点E，连接PB，∠EDB=∠EPB.

（1）求证：PB是的切线；
（2）若PB=6，DB=8，求⊙O的半径

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】已知二次函数y=ax2+bx﹣3a经过点A（﹣1，0）、C（0，3），与x轴交于另一点B，抛物线的顶点为D．

（1）求此二次函数解析式;
（2）连接DC、BC、DB，求证：△BCD是直角三角形;
（3）在对称轴右侧的抛物线上是否存在点P，使得△PDC为等腰三角形？若存在，求出符合条件的点P的坐标；若不存在，请说明理由.

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，一艘海轮在A点时测得灯塔C在它的北偏东42°方向上，它沿正东方向航行80海里后到达B处，此时灯塔C在它的北偏西55°方向上．

（1）求海轮在航行过程中与灯塔C的最短距离（结果精确到0.1）；
（2）求海轮在B处时与灯塔C的距离（结果保留整数）．
（参考数据：sin55°≈0.819，cos55°≈0.574，tan55°≈1.428，tan42°≈0.900，tan35°≈0.700，tan48°≈1.111）

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】小明购买了一部新手机，到某通讯公司咨询移动电话资费情况，准备办理入网手续，该通讯公司工作人员向他介绍两种不同的资费方案：

方案代号	月租费（元）	免费时间（分）	超过免费时间的通话费（元/分）
一	10	0	0.20
二	30	80	0.15

（1）分别写出方案一、二中，月话费（月租费与通话费的总和）y（单位：元）与通话时间x（单位：分）的函数关系式；
（2）画出（1）中两个函数的图象；
（3）若小明月通话时间为200分钟左右，他应该选择哪种资费方案最省钱．

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学