
����Ŀ������֪������ֱ���ҵ�ֱ��ƽ�������ң�����ƽ�����������Ե���������ƽ�ֻ���ֱ����ֱƽ�����������Ե��ң������������һ���۽�����⣺
��ͼ����P����MN���ϱ�����Ϊֱ���ġ�O�ϣ�MN=8��PQ��MN����O�ڵ�Q������ΪH��PQ��MN����PC��PD�ֱ�MN�ڵ�E��F����PE=PF��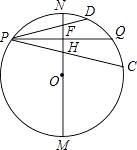
��1���Ƚ� ![]() ��
�� ![]() �Ĵ�С��
�Ĵ�С��
��2����OH=2 ![]() ����֤��OP��CD��
����֤��OP��CD��
��3����ֱ��MN��CD�ཻ���ɵ����Ϊ������ȷ��cos��= ![]() ʱ����P��λ�ã�
ʱ����P��λ�ã�
���𰸡�
��1���⣺��PE=PF��PH��EF��
��PHƽ�֡�FPE��
���DPQ=��CPQ��
�� ![]() =
= ![]() ��
��
��2��֤��������CD��OP��OQ��OQ��CD��B����ͼ��
��OH=2 ![]() ��OP=4��
��OP=4��
��PH= ![]() =2
=2 ![]() ��
��
���OPHΪ����ֱ�������Σ�
���OPQ=45�㣬
��OP=OQ��
���OPQΪ����ֱ�������Σ�
���POQ=90�㣬
��OP��OQ��
�� ![]() =
= ![]() ��
��
��OQ��CD��
��OP��CD
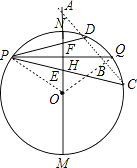
��3���⣺ֱ��CD��MN��A����ͼ��
��cos��= ![]() ��
��
��Ϧ�=30�㣬��ֱ��MN��CD�ཻ���ɵ����Ϊ30�㣬
��OB��CD��
���AOB=60�㣬
��OH��PQ��
���POH=60�㣬
��Rt��POH����sin��POH= ![]() ��
��
��PH=4sin60��=2 ![]() ��
��
����P��MN�ľ���Ϊ2 ![]() ��
��

����������1�����ݵ��������ε����ʣ���PE=PF��PH��EF���ж�PHƽ�֡�FPE��Ȼ�����Բ�нǶ����õ� ![]() =
= ![]() ����2������CD��OP��OQ��OQ��CD��B����ͼ���ȼ����PH=2
����2������CD��OP��OQ��OQ��CD��B����ͼ���ȼ����PH=2 ![]() ������жϡ�OPHΪ����ֱ�������εõ���OPQ=45�㣬���жϡ�OPQΪ����ֱ�������εõ���POQ=90�㣬Ȼ����ݴ�����������
������жϡ�OPHΪ����ֱ�������εõ���OPQ=45�㣬���жϡ�OPQΪ����ֱ�������εõ���POQ=90�㣬Ȼ����ݴ����������� ![]() =
= ![]() �õ�OQ��CD�������ƽ���ߵ��ж�������OP��CD����3��ֱ��CD��MN��A����ͼ��������ǵ����Ǻ���ֵ�áϦ�=30�㣬��ֱ��MN��CD�ཻ���ɵ����Ϊ30�㣬����OB��CD�õ���AOB=60�㣬���POH=60�㣬Ȼ����Rt��POH���������ҵĶ�������PH���ɣ����⿼����Բ���ۺ��⣺�������մ�����������������Բ�ܽǶ������ܹ����Ӧ�õ���ֱ�������ε����ʺ����Ǻ������м��μ��㣮
�õ�OQ��CD�������ƽ���ߵ��ж�������OP��CD����3��ֱ��CD��MN��A����ͼ��������ǵ����Ǻ���ֵ�áϦ�=30�㣬��ֱ��MN��CD�ཻ���ɵ����Ϊ30�㣬����OB��CD�õ���AOB=60�㣬���POH=60�㣬Ȼ����Rt��POH���������ҵĶ�������PH���ɣ����⿼����Բ���ۺ��⣺�������մ�����������������Բ�ܽǶ������ܹ����Ӧ�õ���ֱ�������ε����ʺ����Ǻ������м��μ��㣮


 �̲�ȫ���ִʾ�ƪϵ�д�
�̲�ȫ���ִʾ�ƪϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����
��1���Ķ����⣺
��ͼ�٣��ڡ�ABC�У���AB=10��AC=6����BC���ϵ�����AD��ȡֵ��Χ��
�����������������·������ӳ�AD����EʹDE=AD��������BE����ACD���ŵ�D��ʱ����ת180��õ���EBD������AB��AC��2AD�����ڡ�ABE�У��������������ߵĹ�ϵ�����жϣ�
����AD��ȡֵ��Χ����
��2����������
��ͼ�ڣ��ڡ�ABC�У�D��BC���ϵ��е㣬DE��DF�ڵ�D��DE��AB�ڵ�E��DF��AC�ڵ�F������EF����֤��BE+CF��EF��
��3��������չ��
��ͼ�ۣ����ı���ABCD�У���B+��D=180�㣬CB=CD����BCD=140�㣬��CΪ������һ��70��ǣ��ǵ����߷ֱ�AB��AD��E��F���㣬����EF��̽���߶�BE��DF��EF֮���������ϵ��������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx��4��a��0����x�ύ��A��4��0����B����1��0�����㣬����A��ֱ��y=��x+4���������ڵ�C��
��1����������ߵĽ���ʽ��
��2����ֱ��AC����һ����E������E��ij��λ��ʱ��ʹ��BDE���ܳ���С�����ʱE�����ꣻ
��3��������E��ֱ��AC��������Χ�ɵķ����A��C��B��D��A���˶�ʱ���Ƿ����ʹ��BDEΪֱ�������ε�����������ڣ���ֱ��д������Ҫ���E������ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ȷ������ �� ��
A. ������������һ������ B. ����ͼ�ξ���λ��ͼ��
C. ���![]() �����߶�
�����߶�![]() �Ļƽ�ָ�㣬��ô
�Ļƽ�ָ�㣬��ô![]() D. ��һ�������ȵ�����ֱ������������
D. ��һ�������ȵ�����ֱ������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�Ա���������![]() ��
��![]() ����
����![]() �������Ͻ������ۣ�
�������Ͻ������ۣ�![]() ��
��![]() ��ÿ���۸�
��ÿ���۸�![]() Ԫ,
Ԫ,![]() ��
��![]() ��ÿ���۸�
��ÿ���۸�![]() Ԫ,��һ��������
Ԫ,��һ��������![]() ��.
��.
��1�����Ա�������һ��������![]() �����ܷ��ò�����
�����ܷ��ò�����![]() Ԫ����
Ԫ����![]() ��
��![]() �����ٹ�����ټ���
�����ٹ�����ټ���
��2����������������ã����Ա��������㹺���ڶ���![]() ����������
����������![]() ��
��![]() ����
����![]() ������֮��Ϊ
������֮��Ϊ![]() ���۸ֵ�һ���ļ۸䣻����������
���۸ֵ�һ���ļ۸䣻����������![]() ��
��![]() ���ļ۸��ڵ�һ������ļ۸���ÿ��������
���ļ۸��ڵ�һ������ļ۸���ÿ��������![]() Ԫ��
Ԫ��![]() ��
��![]() ���ļ۸�ȵ�һ�������ļ۸���ÿ��������
���ļ۸�ȵ�һ�������ļ۸���ÿ��������![]() Ԫ��
Ԫ��![]() ��
��![]() ���������ȵڶ���������
���������ȵڶ���������![]() ��
��![]() ��
��![]() ���������ȵڶ���������
���������ȵڶ���������![]() ,�ڶ����������������
,�ڶ����������������![]() �����ܷ�����ͬ,��
�����ܷ�����ͬ,��![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��BE��CD��BE=DE��BC=DA��
��֤����1����BEC�ա�DAE��
��2��DF��BC��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ABCD�У���A=30�㣬��ͬһƽ���ڣ��ԶԽ���BDΪ�ױ�������Ϊ120��ĵ���������BDE�����EBC�Ķ���Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧϰ��Ϊ�ִ��˵�ʱ�У�ij���йز���ͳ�������6���µ�ͼ��ݵĶ��ߵ�ְҵ�ֲ����������������������������ͳ��ͼ�� 
��1����ͳ�Ƶ����ʱ���ڣ��������˴ε�ͼ����Ķ�����������ռ�ٷֱ�Ϊ%��
��2��������ͳ��ͼ����������
��3����5�·ݵ�ͼ��ݵĶ��߹�28000�˴Σ���������Լ�ж����˴ζ�����ְ����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com