
【题目】如图1,在△ABO中,∠OAB=90°,∠AOB=30°,OB=8.以OB为一边,在△OAB外作等边三角形OBC,D是OB的中点,连接AD并延长交OC于E. 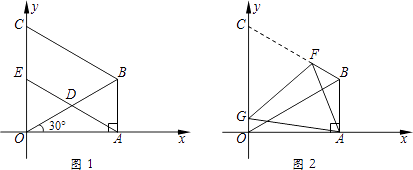
(1)求点B的坐标;
(2)求证:四边形ABCE是平行四边形;
(3)如图2,将图1中的四边形ABCO折叠,使点C与点A重合,折痕为FG,求OG的长.
【答案】
(1)解:在△OAB中,∠OAB=90°,∠AOB=30°,OB=8,
∴OA=OBcos30°=8× ![]() =4
=4 ![]() ,
,
AB=OBsin30°=8× ![]() =4,
=4,
∴点B的坐标为(4 ![]() ,4)
,4)
(2)证明:∵∠OAB=90°,
∴AB⊥x轴,
∵y轴⊥x轴,
∴AB∥y轴,即AB∥CE,
∵∠AOB=30°,
∴∠OBA=60°,
∵DB=DO=4
∴DB=AB=4
∴∠BDA=∠BAD=120°÷2=60°,
∴∠ADB=60°,
∵△OBC是等边三角形,
∴∠OBC=60°,
∴∠ADB=∠OBC,
即AD∥BC,
∴四边形ABCE是平行四边形
(3)解:设OG的长为x,
∵OC=OB=8,
∴CG=8﹣x,
由折叠的性质可得:AG=CG=8﹣x,
在Rt△AOG中,AG2=OG2+OA2,
即(8﹣x)2=x2+(4 ![]() )2,
)2,
解得:x=1,
即OG=1
【解析】(1)由在△ABO中,∠OAB=90°,∠AOB=30°,OB=8,根据三角函数的知识,即可求得AB与OA的长,即可求得点B的坐标;(2)首先可得CE∥AB,D是OB的中点,根据直角三角形斜边的中线等于斜边的一半,可证得BD=AD,∠ADB=60°,又由△OBC是等边三角形,可得∠ADB=∠OBC,根据内错角相等,两直线平行,可证得BC∥AE,继而可得四边形ABCD是平行四边形;(3)首先设OG的长为x,由折叠的性质可得:AG=CG=8﹣x,然后根据勾股定理可得方程(8﹣x)2=x2+(4 ![]() )2 , 解此方程即可求得OG的长.
)2 , 解此方程即可求得OG的长.


科目:初中数学 来源: 题型:
【题目】如下图,下列四个几何体中,它们各自的三视图(主视图、左视图、俯视图)有两个相同,而另一个不同的几何体是 ( )
A.①②
B.②③
C.②④
D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我市开展的“阳光体育”跳绳活动中,为了了解中学生跳绳活动的开展情况,随机抽查了全市八年级部分同学1分钟跳绳的次数,将抽查结果进行统计,并绘制两个不完整的统计图.请根据图中提供的信息,解答下列问题:
(1)本次共抽查了多少名学生?
(2)请补全频数分布直方图空缺部分,直接写出扇形统计图中跳绳次数范围135≤x≤155所在扇形的圆心角度数.
(3)若本次抽查中,跳绳次数在125次以上(含125次)为优秀,请你估计全市8000名八年级学生中有多少名学生的成绩为优秀?
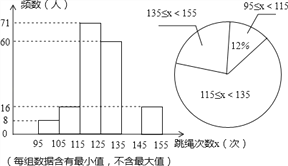
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在平行四边形ABCD中,对角线AC与BD交于点O,过点O的直线EF分别与AD、BC交于点E、F,EF⊥AC,连结AF、CE.
(1)求证:OE=OF;
(2)请判断四边形AECF是什么特殊四边形,请证明你的结论.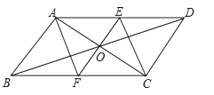
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com