
����Ŀ����ͼ������������MNPQ�У�ÿ��С����ı߳�����ȣ�������ABCD�Ķ�����������MNPQ��4���ߵ�С�����ϣ�

(1)��������MNPQ�����ڵ�ÿ��С����ı߳�Ϊ1����
�١�ABQ����BCM����CDN����ADP�������
��������ABCD�������
(2)��MB��a��BQ��b���������ͼ���е�ֱ�������κ������ε������ϵ��������֤��ѧ������һ����ѧ��ʽ������
���𰸡���1����S��ABQ��6�� S��BCM��6�� S��CDN��6�� S��ADP��6����S������ABCD��25����2����֤�˹��ɶ�����֤�������������.
��������
��1���ٸ���ֱ�������ε������ʽ���ɵó������
��������ó�S������ABCD=S������MNPQ��4S��ABQ�����ɵó������
��2����Ȼ��������ܹ���֤���ɶ�����
��1���١�������ÿ��С�����εı߳�Ϊ1����ͼ��֪AQ=3��BQ=4����Q=90�㣬��S��ABQ![]() AQBQ=6��ͬ��S��BCM=S��CDN=S��ADP=6��
AQBQ=6��ͬ��S��BCM=S��CDN=S��ADP=6��
�ڡ�MQ=7����S������MNPQ=72=49����S������ABCD=S������MNPQ��4S��ABQ=49��4��6=25��
��2����֤���ɶ�����
��֤���ڡ�BCM�͡�ABQ�У���BM=AQ����M=��Q��CM=BQ�����BCM�ա�ABQ��SAS����ͬ����CDN�ա�DAP�ա�BCM��
��S������ABCD=S������MNPQ��4S��ABQ
��AB2=��a+b��2��4![]() ab����AB2=a2+b2��
ab����AB2=a2+b2��
��AB=c���ã�c2=a2+b2�����ɶ�������


 ��һ����ͬ���ɽ�����ϵ�д�
��һ����ͬ���ɽ�����ϵ�д� ������Ӧ���ϵ�д�
������Ӧ���ϵ�д� ��ʦ�㾦�ִʾ��ƪϵ�д�
��ʦ�㾦�ִʾ��ƪϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AB=6��BC=4�����Խ���BD�е�O��ֱ�߷ֱ�AB��CD���ڵ�E��F��
��1����֤���ı���BEDF��ƽ���ı��Σ�
��2�����ı���BEDF������ʱ����EF�ij���
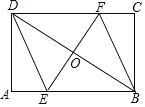
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����OΪ�ȱ�������ABC��һ�㣬����OA��OB��OC����OBΪһ������OBM��60�㣬��BO��BM������CM��OM.
(1)�ж�AO��CM�Ĵ�С��ϵ��֤����
(2)��OA��8��OC��6��OB��10���жϡ�OMC����״��֤����
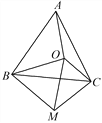
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��̽������ͼ1��ֱ��l���������������ֱ���A��B���㣬�뷴��������y= ![]() ��k��0��x��0����ͼ����C��D���㣨��C�ڵ�D����ߣ�������C��CE��y���ڵ�E������D��DF��x���ڵ�F��CE��DF���ڵ�G��a��b����
��k��0��x��0����ͼ����C��D���㣨��C�ڵ�D����ߣ�������C��CE��y���ڵ�E������D��DF��x���ڵ�F��CE��DF���ڵ�G��a��b����
��1���� ![]() �����ú�n�Ĵ���ʽ��ʾ
�����ú�n�Ĵ���ʽ��ʾ ![]() ��
��
��2����֤��AC=BD��
Ӧ�ã���ͼ2��ֱ��l���������������ֱ��ڵ�A��B���㣬�뷴��������y= ![]() ��k��0��x��0����ͼ���ڵ�C��D���㣨��C�ڵ�D����ߣ�����֪
��k��0��x��0����ͼ���ڵ�C��D���㣨��C�ڵ�D����ߣ�����֪ ![]() ����OBD�����Ϊ1�����ú�m�Ĵ���ʽ��ʾk��
����OBD�����Ϊ1�����ú�m�Ĵ���ʽ��ʾk��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳����ۼס�������Ʒ�Ƶ������ֻ����������ֻ��Ľ��ۺ��ۼ����±���
�� | �� | |
���ۣ�Ԫ/���� | 4000 | 2500 |
�ۼۣ�Ԫ/���� | 4300 | 3000 |
���̳��ƻ����������ֻ����ɲ�������15.5��Ԫ��Ԥ��ȫ�����ۺ�ɻ�ë����2.1��Ԫ��
��ë����=���ۼ۩����ۣ�����������
��1�����̳��ƻ������ס��������ֻ������ٲ���
��2��ͨ���г����У����̳�������ԭ�ƻ��Ļ����ϣ����ټ����ֻ��Ĺ������������������ֻ��Ĺ�����������֪�����ֻ����ӵ������Ǽ����ֻ����ٵ�������2�����������ڹ����������ֻ������ʽ���16��Ԫ�����̳�����������ʹȫ�����ۺ��õ�ë�������������ë����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ����BC�ǡ�O���ң��뾶OD��BC������ΪE����BC= ![]() ��DE=3��
��DE=3��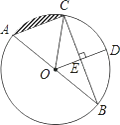
��
��1����O�İ뾶��
��2����AC�ij���
��3����Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ�ߺ�Բ����һ���ǵ�����֪�ǣ���ͼ���ܵó��������ǣ�������

A. SAS B. SSS C. AAS D. ASA
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������ʦ����˶��ֻ����п��߶��������ζ�����������������һ�ζ�����ȣ�����ʦ�ڶ��ζ������������İٷ�������ƽ���������ٵİٷ��ʵ�3����������ʦ�ڶ��ζ���ʱƽ���������ٵİٷ���Ϊx��0��x��0.5����
��Ŀ | ��һ�ζ��� | �ڶ��ζ��� |
���������� | 10000 | �� |
ƽ����������/���� | 0.6 | �� |
���루�ף� | 6000 | 7020 |
ע��������ƽ������=���룮
��1������������ɱ�����գ�
��2����x��
��3������ʦ���ֺ����в���������һΪ24000������������ζ���������������500�ף�ʹ���ܲ���ǡ��Ϊ24000����������ʦ��500��ƽ��������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com