
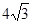 时,求x的值.
时,求x的值.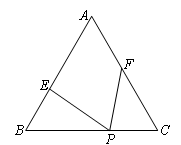
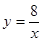 , x的取值范围是
, x的取值范围是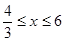 ;(2) ①4,②存在,x=2,
;(2) ①4,②存在,x=2,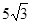 .
.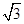 ,EN=
,EN=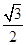 x,CF=y=
x,CF=y=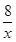 ,FM=
,FM=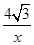 ,根据S四边形AEPF=S△ABC-S△BEP-S△CFP得出方程,求出x即可;
,根据S四边形AEPF=S△ABC-S△BEP-S△CFP得出方程,求出x即可;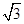 -
-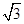 x-
x-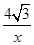 化成-
化成-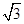 (
(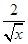 -
-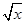 )2+5
)2+5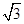 ,即可得出答案.
,即可得出答案.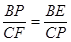
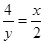
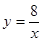 , x的取值范围是
, x的取值范围是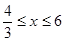 .
.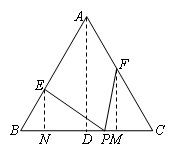
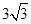 , EN=sin60°×x=
, EN=sin60°×x=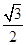 x
x 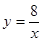 ∴FM=sin60°×
∴FM=sin60°×
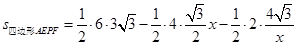
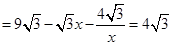 .
.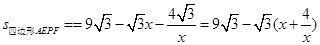
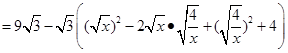
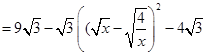
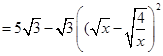
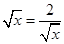 ,即x=2时,四边形AEPF的面积存在最大值,最大值是
,即x=2时,四边形AEPF的面积存在最大值,最大值是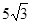 .
.

科目:初中数学 来源:不详 题型:解答题
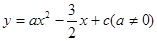 的图象与
的图象与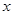 轴交于
轴交于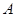 、
、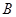 两点,与
两点,与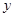 轴交于
轴交于 点,已知点
点,已知点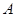 (-1,0),点C(0,-2).
(-1,0),点C(0,-2).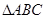 的外接圆的圆心位置,并求出圆心坐标;
的外接圆的圆心位置,并求出圆心坐标;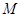 是线段
是线段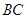 下方的抛物线上的一个动点,求
下方的抛物线上的一个动点,求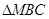 面积的最大值以及此时点
面积的最大值以及此时点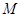 的坐标.
的坐标.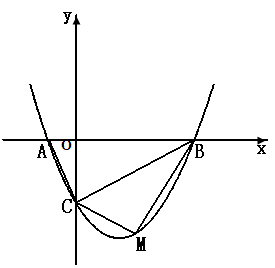
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 =7.14,
=7.14, =7.21,
=7.21, =7.28,
=7.28,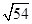 =7.35)
=7.35)
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
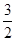 ),点M是抛物线C2:y=mx2-2mx-3m(m<0)的顶点.
),点M是抛物线C2:y=mx2-2mx-3m(m<0)的顶点.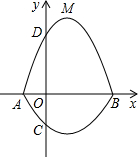
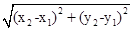 .
.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 的最小值”提出各自的想法.甲说:“可以利用已经学过的完全平方公式,把它配方成
的最小值”提出各自的想法.甲说:“可以利用已经学过的完全平方公式,把它配方成 ,所以代数式的最小值为-2”.乙说:“我也用配方法,但我配成
,所以代数式的最小值为-2”.乙说:“我也用配方法,但我配成 ,最小值为2”.你认为( )
,最小值为2”.你认为( )| A.甲对 | B.乙对 | C.甲、乙都对 | D.甲乙都不对 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
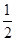 x2-7x+
x2-7x+ ,若自变量x分别取x1,x2,x3,且0<x1<x2<x3,则对应的函数值y1,y2,y3的大小关系正确的是( )
,若自变量x分别取x1,x2,x3,且0<x1<x2<x3,则对应的函数值y1,y2,y3的大小关系正确的是( )| A.y1>y2>y3 | B.y1<y2<y3 |
| C.y2>y3>y1 | D.y2<y3<y1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com