Question

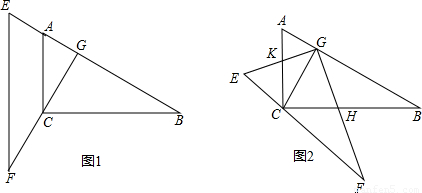
如图1，把两个全等的三角板ABC、EFG叠放在一起，使三角板EFG的直角边FG经过三角板ABC的直角顶点C，垂直AB于G，其中∠B=∠F=30°，斜边AB和EF均为4．现将三角板EFG由图1所示的位置绕G点沿逆时针方向旋转α（0＜α＜90°），如图2，EG交AC于点K，GF交BC于点H．在旋转过程中，请你解决以下问题：

（1）GH∶GK的值是否变化？证明你的结论；

（2）连结HK，求证：KH∥EF；

（3）设AK＝x，请问是否存在x，使△CKH的面积最大，若存在，求x的值，若不存在，请说明理由．

 

Answer 1

（1）解：GH∶GK的值不变，GH∶GK＝．                    

证明如下：∵CG⊥AB，∴∠AGC=∠BGC=90°．

∵∠B=30°，∠ACB=90°，∴∠A=∠GCH=60°．

∵∠AGB=∠BGC=90°，

∴∠AGK=∠CGH．

∴△AGK∽△CGH．∴．                             

∵在Rt△ACG中，tan∠A＝，

∴GH∶GK＝．                                             

 

（2）证明：由（1）得，在Rt△KHG中，tan∠GKH＝，∴∠GKH＝60°．

∵在△EFG中，∠E=∠EGF－∠F=90°－30°＝60°，

∴∠GKH＝∠E．

∴KH∥EF．                                                       

（3）解：存在x=1，使△CKH的面积最大．理由如下：                 

由（1）得△AGK∽△CGH，∴，∴．

在Rt△EFG中，∠EGF =90°，∠F=30°，∴AC＝EF=2，

∴CK=AC－AK=2－x．                                             

∴．

∴当x=1时，△CKH的最大面积为．